题目内容
7.如图1,是一个长为2m、宽为2n的长方形,沿图中虚线剪成四个完全一样的小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的面积为(m-n)2或(m+n)2-4mn;
(2)用两种不同的方法计算图2中阴影部分的面积,可以得到的等式是③(只填序号);
①(m+n)2=m2+2mn+n2 ②(m-n)2=m2-2mn+n2 ③(m-n)2=(m+n)2-4mn
(3)若x-y=-4,xy=$\frac{9}{4}$,则x+y=±5.
分析 (1)根据图形中各个部分的面积得出即可;
(2)根据(1)中的结果即可得出答案;
(3)先根据(2)的结果进行变形,再代入求出即可.
解答 解:(1)图中阴影部分的面积为(m-n)2或(m+n)2-4mn,
故答案为:(m-n)2或(m+n)2-4mn;
(2)(m-n)2=(m+n)2-4mn,
故选③;
(3)∵x-y=-4,xy=$\frac{9}{4}$,
∴(x+y)2=(x-y)2+4xy=(-4)2+4×$\frac{9}{4}$=25,
∴x+y=±5,
故答案为:±5.
点评 本题考查了完全平方公式的应用,能熟记完全平方公式是解此题的关键,注意:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,(a-b)2=(a+b)2-4ab.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.在下列长度的各组线段中,不能构成直角三角形的是( )
| A. | 3,4,5 | B. | $\sqrt{5}$,$\sqrt{12}$,$\sqrt{13}$ | C. | 1,$\sqrt{3}$,2 | D. | 4,5,$\sqrt{41}$ |
15. 如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
 如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )
如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )| A. | AD∥BC | B. | ∠B=∠C | C. | ∠2+∠B=180° | D. | AB∥CD |
17.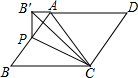 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP沿CP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP的长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP沿CP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP的长度为( )
 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP沿CP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP的长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP沿CP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP的长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
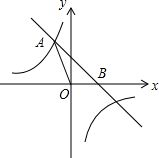 如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B.
如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B.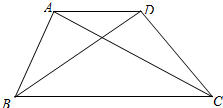 已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求:
已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求: