题目内容
20.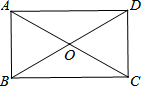 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=2,求AD的长.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=2,求AD的长.
分析 根据矩形的性质得出OA=OB=OC=OD,∠BAD=90°,求出△AOB是等边三角形,求出OB=AB=2,根据矩形的性质求出BD,根据勾股定理求出AD即可.
解答 解:∵四边形ABCD是矩形,
∴OA=OB=OC=OD,∠BAD=90°,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=2,
∴BD=2BO=4,
在Rt△BAD中,AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 本题考查了矩形的性质,等边三角形的性质和判定,勾股定理的应用,能熟记矩形的性质是解此题的关键.

练习册系列答案
相关题目
8. 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
 如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )
如图,点O在直线AB上,且OC⊥OD.若么∠BOD=55°,则∠COA的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
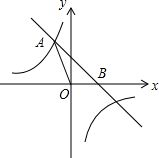 如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B.
如图,直线y=-x+b与反比例函数$y=-\frac{3}{x}$的图象相交于点A(a,3),且与x轴相交于点B. 如图,一个机器人从点O出发,向正东方向走3米到达点A1,再向正北方向走6米到达点A2,再向正西方向走9米到达点A3,再向正南方向走12米到达点A4,再向正东方向走15米到达点A5…按此规律走下去,当机器人走到点A6时,所在的位置是(9,12)(用坐标表示)
如图,一个机器人从点O出发,向正东方向走3米到达点A1,再向正北方向走6米到达点A2,再向正西方向走9米到达点A3,再向正南方向走12米到达点A4,再向正东方向走15米到达点A5…按此规律走下去,当机器人走到点A6时,所在的位置是(9,12)(用坐标表示)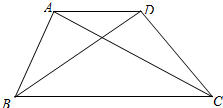 已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求:
已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求: