题目内容
 如图,点E是?ABCD的边CB延长线上一点,EA分别交CD、BD的延长线于点F、G,则图中相似三角形共有( )对.
如图,点E是?ABCD的边CB延长线上一点,EA分别交CD、BD的延长线于点F、G,则图中相似三角形共有( )对.| A、4 | B、5 | C、6 | D、7 |
考点:相似三角形的判定
专题:探究型
分析:先根据平行四边形的性质得BC∥AD,AB∥CD,△ABD∽△CDB,再利用平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,由AB∥CF得到△EAB∽△EFC,由AD∥EC得到△AFD∽△EFC,则△EAD∽△AFD;再由AD∥BE得△ADG∽△EBG;由DF∥AB得到△GDF∽△GBA.
解答:解:∵四边形ABCD为平行四边形,
∴BC∥AD,AB∥CD,△ABD∽△CDB,
∵AB∥CF,
∴△EAB∽△EFC,
∵AD∥EC,
∴△AFD∽△EFC,
∴△EAD∽△AFD;
∵AD∥BE,
∴△ADG∽△EBG;
∵DF∥AB,
∴△GDF∽△GBA.
故选C.
∴BC∥AD,AB∥CD,△ABD∽△CDB,
∵AB∥CF,
∴△EAB∽△EFC,
∵AD∥EC,
∴△AFD∽△EFC,
∴△EAD∽△AFD;
∵AD∥BE,
∴△ADG∽△EBG;
∵DF∥AB,
∴△GDF∽△GBA.
故选C.
点评:本题考查了相似三角形的判定:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.也考查了平行四边形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
两圆的半径R,r分别是方程x2-5x+6=0的两根,两圆圆心距为5,则两圆位置关系是( )
| A、外离 | B、内含 | C、相交 | D、相切 |
如果|
|=3.|
|=2,且
与
反向,那么下列关系中成立的是( )
| a |
| b |
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
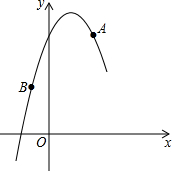 如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )
如图,在平面直角坐标系中,抛物线y=ax2+bx+5经过A(2,5),B(-1,2)两点,若点C在该抛物线上,则C点的坐标可能是( )| A、(-2,0) |
| B、(0.5,6.5) |
| C、(3,2) |
| D、(2,2) |
如果三角形的三个内角的比是3:4:7,那么这个三角形是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形或钝角三角形 |
下列解方程的过程中错误的是( )
| A、方程2x+5=-4,变形为2x=-4+5 |
| B、方程2x-5=-4,变形为2x=-4+5 |
| C、方程3x=8-x,变形为3x+x=8 |
| D、方程8-x=3x,变形为x+3x=8 |

 如图,△ABC和△ABD中,∠C=∠D=Rt∠,E是BC边上的中线.请你说明CE=DE的理由.
如图,△ABC和△ABD中,∠C=∠D=Rt∠,E是BC边上的中线.请你说明CE=DE的理由.