题目内容
已知关于x的方程x2+2x-a+1=0没有实数根，试判断关于x的方程x2+ax+a=1是否一定有两个不相等的实数根，并说明理由．
考点：根的判别式
专题：
分析：根据方程无实数根，可得判别式△＜0，根据a的取值范围，可得第二个方程判别式的情况，可得答案．
解答：解：关于x的方程x2+ax+a=1一定有两个不相等的实数根，理由如下：
由x的方程x2+2x-a+1=0没有实数根，得
△=b2-4ac=4-4（-a+1）＜0，解得a＜0，
由x2+ax+a=1，得
△=b2-4ac=a2-4（a-1）=a2-4a+4=（a-2）2，
∵a＜0，
∴△=（a-2）2＞0，
∴关于x的方程x2+ax+a=1一定有两个不相等的实数根．
由x的方程x2+2x-a+1=0没有实数根，得
△=b2-4ac=4-4（-a+1）＜0，解得a＜0，
由x2+ax+a=1，得
△=b2-4ac=a2-4（a-1）=a2-4a+4=（a-2）2，
∵a＜0，
∴△=（a-2）2＞0，
∴关于x的方程x2+ax+a=1一定有两个不相等的实数根．
点评：本题考查了根的判别式，利用了根方程无实数根时判别式小于零，根的判别式大于零时方程有两不等实数根．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
一工厂计划2007年的成本比2005年的成本降低15%，如果每一年比上一年降低的百分率为x，那么求平均每一年比上一年降低的百分率的方程是（ ）
| A、（1-x）2=15% |
| B、（1+x）2=1+15% |
| C、（1-x）2=1+15% |
| D、（1-x）2=1-15% |
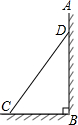如图，一根铁管CD固定在墙角，若BC=5米，∠BCD=55°，则铁管CD的长为（ ）A、
| ||
| B、5•sin55°米 | ||
C、
| ||
| D、5•cos55°米 |
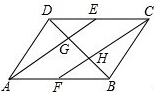如图，已知平行四边形ABCD中，点E、F分别是边DC、AB的中点，AE、CF分别与对角线BD相交于点G、H，设
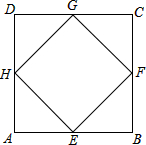（1）如图，顺次连接正方形ABCD的各边中点，得到一个小正方形EFGH．则正方形EFGH与正方形ABCD的面积比是多少？