题目内容
解下列方程
(1)
+
=0;
(2)2x2+4x+1=0.
(1)
| 1 |
| x-1 |
| 3 |
| x |
(2)2x2+4x+1=0.
考点:解分式方程,解一元二次方程-公式法
专题:
分析:(1)根据分式方程两边都乘以x(x-1),可转化成整式方程;
(2)根据公式法,可得一元二次方程的解.
(2)根据公式法,可得一元二次方程的解.
解答:解:(1)方程两边都乘以x(x-1),得
x+3(x-1)=0.解得x=
.检验:当x=
时,x(x-1)≠0,
x=
是原分式方程的解;
(2)2x2+4x+1=0,
a=2,b=4,c=1,△=b2-4ac=16-8=8>0,
x=
=
,x1=
,x2=
.
x+3(x-1)=0.解得x=
| 3 |
| 4 |
| 3 |
| 4 |
x=
| 3 |
| 4 |
(2)2x2+4x+1=0,
a=2,b=4,c=1,△=b2-4ac=16-8=8>0,
x=
-b±
| ||
| 2a |
-4±2
| ||
| 4 |
-2+
| ||
| 2 |
-2-
| ||
| 2 |
点评:本题考查了解分式方程,(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求,(2)解分式方程一定注意要验根..

练习册系列答案
相关题目
下列四个角度不是正多边形内角的是( )
| A、60° | B、108° |
| C、120° | D、155° |
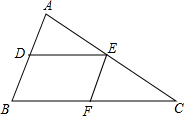 如图,已知DE∥BC,EF∥AB,从下列选项中选择一个正确的并说明理由.
如图,已知DE∥BC,EF∥AB,从下列选项中选择一个正确的并说明理由. 小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明)
小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明)
 已知一次函数的图象经过(6,-3)和(-3,6)两点,
已知一次函数的图象经过(6,-3)和(-3,6)两点,