题目内容
若a2+a-1=0，则a3+2a2+2014= ．
考点：因式分解的应用
专题：
分析：把a3+2a2+2014转化为a（a2+a-1）+（a2+a-1）+2015求解即可．
解答：解：∵a2+a-1=0，
∴a3+2a2+2014=a3+a2-a+a2+a-1+1+2014=a（a2+a-1）+（a2+a-1）+2015=2015．
故答案为：2015．
∴a3+2a2+2014=a3+a2-a+a2+a-1+1+2014=a（a2+a-1）+（a2+a-1）+2015=2015．
故答案为：2015．
点评：本题主要考查了因式分解的应用，解题的关键是利用拆项来构造出a2+a-1这个式子．
练习册系列答案
相关题目
某小区规划在边长为x米的正方形场地修建两条宽两米的小路，如图，其余部分种草，求草地面积．
某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：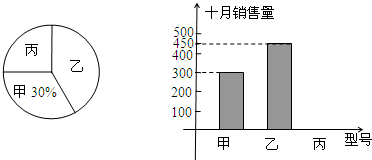
已知△A′B′C′是由△ABC是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如下表所示：
如图，在梯形ABCD中，AD∥BC，EF是中位线，AF平分∠BAD．求证：AB=2EF．