题目内容
商场经营某品牌服装,去年11月份的销量为100件,为了扩大销量,12月商场对这种服装打9折销售,结果销量增加了50%,销售额增加了28000元.
(1)求该服装去年11月份的销售单价和销售额各是多少;
(2)若去年11月份销售这种服装获利20000元,今年1月份全月商场为迎新年进行促销,此服装在去年11月销售价的基础上一律打8折销售,若该服装成本不变,则销量至少为多少件,才能保证今年1月的利润比去年11月利润至少增加25%?
(1)求该服装去年11月份的销售单价和销售额各是多少;
(2)若去年11月份销售这种服装获利20000元,今年1月份全月商场为迎新年进行促销,此服装在去年11月销售价的基础上一律打8折销售,若该服装成本不变,则销量至少为多少件,才能保证今年1月的利润比去年11月利润至少增加25%?
考点:一元一次方程的应用
专题:应用题
分析:(1)该服装去年11月份的销售单价为每件x元,利用两个月销售额的差列方程得到100(1+50%)×90%-100x=28000,解得x=800,然后计算100x即可;
(2)设每件的成本为y元,利用每件的利润×销售量得到总利润得(800-y)×100=20000,解得y=600(元);再设今年1月份的销售数量为a件,根据今年1月的利润比去年11月利润至少增加25%得到(800×80%-600)≥20000(1+25%),然后解不等,再求出最小值即可.
(2)设每件的成本为y元,利用每件的利润×销售量得到总利润得(800-y)×100=20000,解得y=600(元);再设今年1月份的销售数量为a件,根据今年1月的利润比去年11月利润至少增加25%得到(800×80%-600)≥20000(1+25%),然后解不等,再求出最小值即可.
解答:解:(1)该服装去年11月份的销售单价为每件x元,
根据题意得100(1+50%)×90%-100x=28000,解得x=800,
所以该服装去年11月份的销售单价为每件800元,
该服装去年11月份的销售额=800元×100=80000元;
(2)设每件的成本为y元,
根据题意得(800-y)×100=20000,解得y=600(元);
设今年1月份的销售数量为a件,
根据题意得(800×80%-600)≥20000(1+25%),
解得a≥625.
答:该服装成本不变,则销量至少为625件,才能保证今年1月的利润比去年11月利润至少增加25%.
根据题意得100(1+50%)×90%-100x=28000,解得x=800,
所以该服装去年11月份的销售单价为每件800元,
该服装去年11月份的销售额=800元×100=80000元;
(2)设每件的成本为y元,
根据题意得(800-y)×100=20000,解得y=600(元);
设今年1月份的销售数量为a件,
根据题意得(800×80%-600)≥20000(1+25%),
解得a≥625.
答:该服装成本不变,则销量至少为625件,才能保证今年1月的利润比去年11月利润至少增加25%.
点评:本题考查了一元一次方程的应用:利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.

练习册系列答案
相关题目
 一个几何体如图所示,那么它的俯视图是( )
一个几何体如图所示,那么它的俯视图是( )A、 |
B、 |
C、 |
D、 |
关于函数y=3x+1,下列结论错误的是( )
| A、图象必经过点(-2,1) | ||
| B、y值x的增大而增大 | ||
| C、图象必经过第一、二、三象限 | ||
D、当x>-
|
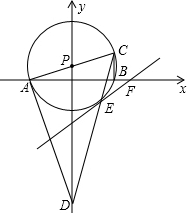 如图,已知P(0,1),⊙P与x轴交于A、B两点,AC是⊙P的直径,OA、OD的长是关于x的方程x2-3kx+2k2=0的两根,且OA2+OD2=20.
如图,已知P(0,1),⊙P与x轴交于A、B两点,AC是⊙P的直径,OA、OD的长是关于x的方程x2-3kx+2k2=0的两根,且OA2+OD2=20.