题目内容
9.$\sqrt{1+x}•\sqrt{1-x}=\sqrt{1-{x}^{2}}$成立的条件是-1≤x≤1.分析 直接利用二次根式的性质结合不等式组的解法求出答案.
解答 解:∵$\sqrt{1+x}•\sqrt{1-x}=\sqrt{1-{x}^{2}}$成立,
∴$\left\{\begin{array}{l}{1+x≥0}\\{1-x≥0}\end{array}\right.$,
解得:-1≤x≤1.
故答案为:-1≤x≤1.
点评 此题主要考查了二次根式的性质,正确得出关于x的不等式组是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.计算:(-2a)2•(-3a)3的结果是( )
| A. | -108a5 | B. | -108a6 | C. | 108a5 | D. | 108a6 |
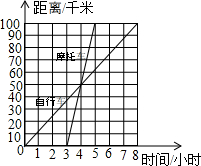 如图所示,是一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象填空:
如图所示,是一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象填空: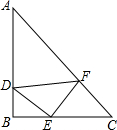 如图,△ABC、△DEF都是等腰三角形,D、E、F分别在AB、BC、CA上,已知:∠B=∠DEF=90°,AB=BC,DE=EF.
如图,△ABC、△DEF都是等腰三角形,D、E、F分别在AB、BC、CA上,已知:∠B=∠DEF=90°,AB=BC,DE=EF. 如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.
如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.