题目内容
已知关于x的方程
(1-x)=1+k的解与
(x-1)-
k=
(x-1)的解互为相反数,求k.
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 2 |
| 3 |
考点:一元一次方程的解
专题:计算题
分析:分别表示出已知两方程的解,根据两方程的解互为相反数列出关于k的方程,求出方程的解即可得到k的值.
解答:解:方程
(1-x)=1+k,
去分母得:1-x=2+2k,
解得:x=-2k-1;
方程
(x-1)-
k=
(x-1),
去分母得:9x-9-18k=8x-8,
解得:x=18k+1,
由两方程的解互为相反数,得到-2k-1+18k+1=0,
解得:k=0.
| 1 |
| 2 |
去分母得:1-x=2+2k,
解得:x=-2k-1;
方程
| 3 |
| 4 |
| 3 |
| 2 |
| 2 |
| 3 |
去分母得:9x-9-18k=8x-8,
解得:x=18k+1,
由两方程的解互为相反数,得到-2k-1+18k+1=0,
解得:k=0.
点评:此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
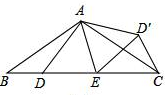 如图,在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E,DE′=DE.
如图,在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E,DE′=DE. 如图,各小方格的边长为1,△ABC的各个顶点都在格点上,求AB边上的高.
如图,各小方格的边长为1,△ABC的各个顶点都在格点上,求AB边上的高.