题目内容
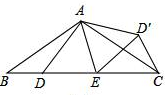如图，在△ABC中，AB=AC，D、E是BC边上的点，将△ABD绕点A旋转，得到△ACD′，连结D′E，DE′=DE．（1）求证：∠BAC=2∠DAE；
（2）若∠BAC=120°，BD与DE满足怎样的数量关系时，△CDE′是直角三角形？请说明理由．
考点：旋转的性质
专题：证明题
分析：（1）根据旋转的性质得AD=AD′，∠BAD=∠CAD′，则∠BAC=∠DAD′，再证明△AED≌△AED′得到∠DAE=∠D′AE，则∠DAD′=2∠DAE，所以∠BAC=2∠DAE；
（2）由∠BAC=120°，AB=AC得∠B=∠ACB=30°，再由旋转的性质得BD=CD′，∠B=∠ACD′=30°，则∠ECD′=∠ECA+∠ACD′=60°，讨论：当∠CED′=90°时，根据含30度的直角三角形三边的关系得到CD′=2CE，D′E=
CE，即BD=2CE，DE=
CE，于是得到BD：DE：CE=2：
：1；同理可得当∠ED′C=90°时，BD：DE：CE=1：
：2．
（2）由∠BAC=120°，AB=AC得∠B=∠ACB=30°，再由旋转的性质得BD=CD′，∠B=∠ACD′=30°，则∠ECD′=∠ECA+∠ACD′=60°，讨论：当∠CED′=90°时，根据含30度的直角三角形三边的关系得到CD′=2CE，D′E=
| 3 |
| 3 |
| 3 |
| 3 |
解答：（1）证明：∵△ABD绕点A旋转，得到△ACD′，
∴AD=AD′，∠BAD=∠CAD′，
∴∠BAC=∠DAD′，
在△AED和△AED′中，
，
∴△AED≌△AED′（SSS），
∴∠DAE=∠D′AE，
∴∠DAD′=2∠DAE，
∴∠BAC=2∠DAE；
（2）解：∵∠BAC=120°，AB=AC，
∴∠B=∠ACB=30°，
∵△ABD绕点A旋转，得到△ACD′，
∴BD=CD′，∠B=∠ACD′=30°，
∴∠ECD′=∠ECA+∠ACD′=60°，
当∠CED′=90°时，则CD′=2CE，D′E=
CE，
∴BD=2CE，DE=
CE，
∴BD：DE：CE=2：
：1；
当∠ED′C=90°时，则CE=2CD′，D′E=
CD′，
∴CE=
BD，DE=
BD，
∴BD：DE：CE=1：
：2，
即BD：DE：CE=2：
：1或BD：DE：CE=1：
：2时，△CDE′是直角三角形．
∴AD=AD′，∠BAD=∠CAD′，
∴∠BAC=∠DAD′，
在△AED和△AED′中，
|
∴△AED≌△AED′（SSS），
∴∠DAE=∠D′AE，
∴∠DAD′=2∠DAE，
∴∠BAC=2∠DAE；
（2）解：∵∠BAC=120°，AB=AC，
∴∠B=∠ACB=30°，
∵△ABD绕点A旋转，得到△ACD′，
∴BD=CD′，∠B=∠ACD′=30°，
∴∠ECD′=∠ECA+∠ACD′=60°，
当∠CED′=90°时，则CD′=2CE，D′E=
| 3 |
∴BD=2CE，DE=
| 3 |
∴BD：DE：CE=2：
| 3 |
当∠ED′C=90°时，则CE=2CD′，D′E=
| 3 |
∴CE=
| 3 |
| 3 |
∴BD：DE：CE=1：
| 3 |
即BD：DE：CE=2：
| 3 |
| 3 |
点评：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质和等腰直角三角形的判定．
练习册系列答案
相关题目