题目内容
 如图,AB是⊙O的弦,⊙O的半径为5,∠AOB=120°,则弦AB的长为
如图,AB是⊙O的弦,⊙O的半径为5,∠AOB=120°,则弦AB的长为考点:垂径定理
专题:
分析:过O作OC⊥AB交AB于C点,由垂径定理可知,OC垂直平分AB,再解直角三角形即可求解.
解答: 解:过O作OC⊥AB交AB于C点,如右图所示:
解:过O作OC⊥AB交AB于C点,如右图所示:
由垂径定理可知,OC垂直平分AB,
∵OA=OB,∠AOB=120°,
∴∠OAB=30°,
∴OC=
OA=
,
∴AC=
=
=
∴AB=5
cm
故答案为:5
,
.
 解:过O作OC⊥AB交AB于C点,如右图所示:
解:过O作OC⊥AB交AB于C点,如右图所示:由垂径定理可知,OC垂直平分AB,
∵OA=OB,∠AOB=120°,
∴∠OAB=30°,
∴OC=
| 1 |
| 2 |
| 5 |
| 2 |
∴AC=
| OA2-OC2 |
52-(
|
5
| ||
| 2 |
∴AB=5
| 3 |
故答案为:5
| 3 |
| 5 |
| 2 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
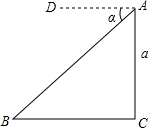 如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )
如图,飞机在空中A处探测得地面目标B处的俯角为α,此时飞机高度为AC=a,则BC的长度是( )| A、a•tanα | ||
B、
| ||
C、
| ||
D、
|
 如图,四边形OEBC为正方形.
如图,四边形OEBC为正方形. 如图,?ABCD中,∠C=108°,BE平分∠ABC,交AD于E,求∠BED的度数.
如图,?ABCD中,∠C=108°,BE平分∠ABC,交AD于E,求∠BED的度数. 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长. 如图,要把边长为6的正三角形剪成一个最大的正六边形,
如图,要把边长为6的正三角形剪成一个最大的正六边形, 如图,添加必要的一个条件,使得AB∥CD,这个条件可以是
如图,添加必要的一个条件,使得AB∥CD,这个条件可以是