题目内容
3.若菱形的两条对角线长分别为10cm和24cm,则顺次连接这个菱形四条边的中点所得的四边形的对角线长是13cm.分析 顺次连接这个菱形各边中点所得的四边形是矩形,且矩形的边长分别是菱形对角线的一半,问题得解.
解答 解:∵顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形;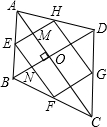
理由如下:
∵E、F、G、H分别为各边中点
∴EF∥GH∥AC,EF=GH=$\frac{1}{2}$DB,
EF=HG=$\frac{1}{2}$AC,EH∥FG∥BD
∵DB⊥AC,
∴EF⊥EH,
∴四边形EFGH是矩形,
∵EH=$\frac{1}{2}$BD=5cm,EF=$\frac{1}{2}$AC=12cm,
∴HF=$\sqrt{E{H}^{2}+E{F}^{2}}$=13cm.
故答案为:13cm.
点评 本题考查菱形的性质,菱形的四边相等,对角线互相垂直,连接菱形各边的中点得到矩形,且矩形的边长是菱形对角线的一半以及勾股定理的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若a2=16,|b|=2,且|a+b|=-(a+b),那么a-b的值只能是( )
| A. | 2 | B. | -2 | C. | 2或-6 | D. | -2或-6 |
15. 如图,已知直线BC,DM相交于点O,OA⊥DM,垂足为O,则∠DOB+∠AOC的度数为( )
如图,已知直线BC,DM相交于点O,OA⊥DM,垂足为O,则∠DOB+∠AOC的度数为( )
 如图,已知直线BC,DM相交于点O,OA⊥DM,垂足为O,则∠DOB+∠AOC的度数为( )
如图,已知直线BC,DM相交于点O,OA⊥DM,垂足为O,则∠DOB+∠AOC的度数为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
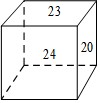 如图,已知一个正方体的六个面上分别写着六个连续的正整数,且每个相对面上的两个数的和都相等,图中所能看到的数是20,23和24,求这六个正整数的和.
如图,已知一个正方体的六个面上分别写着六个连续的正整数,且每个相对面上的两个数的和都相等,图中所能看到的数是20,23和24,求这六个正整数的和.