��Ŀ����
���ж���ʽ������ƽ���ʽ�ֽ���ʽ���ǣ� ��
A��a2+����b��2 B��5m2��20mn C����x2��y2 D����x2+9
 D��
��������
���������A��a2+����b��2������ͬ��������ƽ���ʽ�ֽ���ʽ����Aѡ�����
B��5m2��20mn�������ƽ���������ƽ���ʽ�ֽ���ʽ����Bѡ�����
C����x2��y2������ͬ��������ƽ���ʽ�ֽ���ʽ����Cѡ�����
D����x2+9=��x2+32����������෴������ƽ���ʽ�ֽ���ʽ����Dѡ����ȷ��
��ѡD��
D��
��������
���������A��a2+����b��2������ͬ��������ƽ���ʽ�ֽ���ʽ����Aѡ�����
B��5m2��20mn�������ƽ���������ƽ���ʽ�ֽ���ʽ����Bѡ�����
C����x2��y2������ͬ��������ƽ���ʽ�ֽ���ʽ����Cѡ�����
D����x2+9=��x2+32����������෴������ƽ���ʽ�ֽ���ʽ����Dѡ����ȷ��
��ѡD��
��ϰ��ϵ�д�
�����Ŀ
��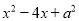 ����ȫƽ��ʽ����ôa����( )
����ȫƽ��ʽ����ôa����( )
A. 4 B. 2 C. ��4 D. ��2
 D
����������x2-4x+a2=x2-2��2•x+a2����a2=22=4����a=��2��
��ѡD��
D
����������x2-4x+a2=x2-2��2•x+a2����a2=22=4����a=��2��
��ѡD�� ������y=x2-4x+m��x���һ�����������Ϊ��1��0���������������x�����һ�������������____
 ��3��0��
���������ѵ㣨1��0������������y=x2-4x+m�У���m=3��
���ԣ�ԭ����Ϊy=x2-4x+3��
��y=0���ⷽ��x2-4x+3=0����x1=1��x2=3
����������x�����һ������������ǣ�3��0����
�ʴ�Ϊ����3��0����
��3��0��
���������ѵ㣨1��0������������y=x2-4x+m�У���m=3��
���ԣ�ԭ����Ϊy=x2-4x+3��
��y=0���ⷽ��x2-4x+3=0����x1=1��x2=3
����������x�����һ������������ǣ�3��0����
�ʴ�Ϊ����3��0���� ���÷ֽ���ʽ���㣺
��1��2022+202��196+982
��2������2��100+����2��100��
 ��1��90000����2��2101��
�������������������1��ͨ���۲죬��Ȼ������ȫƽ����ʽ��������ȫƽ����ʽ�ֽ���ʽ���㣮
��2��������ȡ����ʽ��������ʽ�ֽ���м��㣮
��������
��1��ԭʽ=2022+2��202��98+982
=��202+98��2
=3002
=90000��
��2��ԭʽ=����2��100����1+1��=2101��
��1��90000����2��2101��
�������������������1��ͨ���۲죬��Ȼ������ȫƽ����ʽ��������ȫƽ����ʽ�ֽ���ʽ���㣮
��2��������ȡ����ʽ��������ʽ�ֽ���м��㣮
��������
��1��ԭʽ=2022+2��202��98+982
=��202+98��2
=3002
=90000��
��2��ԭʽ=����2��100����1+1��=2101�� a2��2ab+b2��a2��b2�Ĺ���ʽ��__��
 a��b
����������a2��2ab+b2=(a-b)2��a2��b2=(a+b)(a-b),
��a2��2ab+b2��a2��b2�Ĺ���ʽ��a-b.
a��b
����������a2��2ab+b2=(a-b)2��a2��b2=(a+b)(a-b),
��a2��2ab+b2��a2��b2�Ĺ���ʽ��a-b. ��֪���������ε�һ�߳�����4cm��һ�߳�����9cm���������ܳ���
 22cm
�������������������������ۼ��ɣ�
��������������������
������Ϊ4��4+4<9�����ܹ��������Σ�
������Ϊ9��9-9<4���ܹ��������Σ�9+9+4=22��
���ܳ���22cm��
22cm
�������������������������ۼ��ɣ�
��������������������
������Ϊ4��4+4<9�����ܹ��������Σ�
������Ϊ9��9-9<4���ܹ��������Σ�9+9+4=22��
���ܳ���22cm�� �ȱ���������_________���Գ��ᣬ������__________���Գ���.
 3 2
���������ߵ�����������һ���Գ��ᣬ
��ȱ������ο��Կ����Ը�����Ϊ����ĵ��������Σ�
��ÿһ������¶��ֱ���һ���Գ��ᣬ
��ȱ��������������Գ���.
�ʴ�Ϊ��3��2.
3 2
���������ߵ�����������һ���Գ��ᣬ
��ȱ������ο��Կ����Ը�����Ϊ����ĵ��������Σ�
��ÿһ������¶��ֱ���һ���Գ��ᣬ
��ȱ��������������Գ���.
�ʴ�Ϊ��3��2. ��ͼ����֪�ڵȱ�������ABC�У�D��E�ֱ���AB��AC�ϵĵ㣬��AD��CE.��֤��CD��BE.
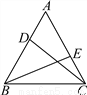
 ������
��������������������ȸ��ݵȱ������ε����ʵó���A=��BCE=60�㣬AC=BC�������֪�����ó���ADC�͡�CEBȫ�ȣ��Ӷ��ó��𰸣�
����������ߡ�ABCΪ�ȱ������Σ� ���A=��BCE=60�㣬AC=BC��
�֡�AD=CE�� ���ADC�ա�CEB(SAS)�� ��CD=BE��
������
��������������������ȸ��ݵȱ������ε����ʵó���A=��BCE=60�㣬AC=BC�������֪�����ó���ADC�͡�CEBȫ�ȣ��Ӷ��ó��𰸣�
����������ߡ�ABCΪ�ȱ������Σ� ���A=��BCE=60�㣬AC=BC��
�֡�AD=CE�� ���ADC�ա�CEB(SAS)�� ��CD=BE�� ��ͼ��ijУ��Χǽ��һ����ͬ�İ�������ɣ��买״ͼ��Ϊ�����ߵ�һ���֣�դ���Ŀ羶AB�䣬����ͬ���0.2����5�������ӹ̣�����OCΪ0.36�ף�������EF�ij�Ϊ��������
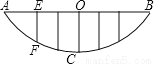
A. 0.4�� B. 0.16�� C. 0.2�� D. 0.24��
 C
����������ͼ����C����ϵ��ԭ�㣬OC����ֱ��Ϊy�Ὠ������ϵ��
�������߽���ʽΪy=ax2������֪��ͼ���B��0.6��0.36��������ã�0.36=0.36a
��a=1����y=x2����F�������Ϊ-0.4���൱x=-0.4ʱ��y=0.16����EF=0.36-0.16=0.2��.��ѡC��
C
����������ͼ����C����ϵ��ԭ�㣬OC����ֱ��Ϊy�Ὠ������ϵ��
�������߽���ʽΪy=ax2������֪��ͼ���B��0.6��0.36��������ã�0.36=0.36a
��a=1����y=x2����F�������Ϊ-0.4���൱x=-0.4ʱ��y=0.16����EF=0.36-0.16=0.2��.��ѡC�� 
