题目内容
用一根长为50 cm的铁丝弯成一个长方形，设这个长方形的一边长为x（cm），它的面积为y（cm2），则y与x之间的函数关系式为（ ）
A. y＝－x2＋50x B. y＝x2－50x C. y＝－x2＋25x D. y＝－2x2＋25
C
【解析】设这个长方形的一边长为xcm，则另一边长为（25-x）cm，根据长方形的面积公式可得y=x（25-x）=－x2＋25x，故选C.
等边三角形有_________条对称轴，矩形有__________条对称轴.
3 2
【解析】∵等腰三角形有一条对称轴，
∴等边三角形可以看成以各个点为顶点的等腰三角形，
而每一种情况下都分别有一条对称轴，
∴等边三角形有三条对称轴.
故答案为：3；2. 如图，某同学在楼房的A处测得荷塘的一端B处的俯角为30°，荷塘另一端D与点C、B在同一条直线上．已知AC＝32米，CD＝16米，则荷塘宽BD为________米(取
≈1.73，结果保留整数)．
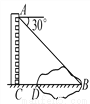
39
【解析】试题分析：根据题意可得：∠B=30°，在Rt△ABC中，tan∠B=tan30°=，则BC=32≈55米，则BD=BC-CD=55-16=39米． 如图，某校的围墙由一段相同的凹曲拱组成，其拱状图形为抛物线的一部分，栅栏的跨径AB间，按相同间隔0.2米用5根立柱加固，拱高OC为0.36米，则立柱EF的长为（ ）
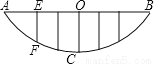
A. 0.4米 B. 0.16米 C. 0.2米 D. 0.24米
C
【解析】如图，以C坐标系的原点，OC所在直线为y轴建立坐标系，
设抛物线解析式为y=ax2，由题知，图象过B（0.6，0.36），代入得：0.36=0.36a
∴a=1，即y=x2．∵F点横坐标为-0.4，∴当x=-0.4时，y=0.16，∴EF=0.36-0.16=0.2米.故选C． 如图，二次函数y= -x2-2x的图象与x轴交于点A、O，在抛物线上有一点P，满足
S△AOP=3，则点P的坐标是（ ）
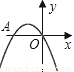
A. （-3，-3） B. （1，-3） C. （-3，-3）或（-3，1） D. （-3，-3）或（1，-3）
D
【解析】分析：根据抛物线的解析式，即可确定点A的坐标，由于OA是定长，根据△AOP的面积即可确定P点纵坐标的绝对值，将其代入抛物线的解析式中，即可求得P点的坐标．
解答：【解析】
抛物线的解析式中，令y=0，得：-x2-2x=0，解得x=0，x=-2；
∴A（-2，0），OA=2；
∵S△AOP=OA?|yP|=3，∴|yP|=3；
当P点纵坐标为3时，-x2-... 如果一个二次函数的图象经过点A(6，10)，与x轴交于B，C两点，点B，C的横坐标分别为x1，x2，且x1＋x2＝6，x1x2＝5，求这个二次函数的解析式．
解析式为y＝2x2－12x＋10．
【解析】试题分析：设交点式为y=a（x﹣x1）（x﹣x2），再展开合并后把x1+x2=6，x1x2=5代入可得y=a（x2﹣6x+5），然后把A点坐标代入求出a的值即可．
试题解析：【解析】
∵抛物线与x轴交于B，C两点，点B，C的横坐标分别为x1，x2，∴抛物线解析式可设为y=a（x﹣x1）（x﹣x2）=a[x2﹣（x1+x2）x+x1x2]，而... 若抛物线y=kx2－2x＋l与x轴有两个交点，则k的取值范围是____．
k＜1，且k≠0
【解析】【解析】
∵y=kx2﹣2x+1为二次函数，∴k≠0．
∵抛物线y=kx2﹣2x+1的图象与x轴有两个交点，∴△＞0，即（﹣2）2－4k＞0．
解得：k＜1，∴k的取值范围是k＜1且k≠0．
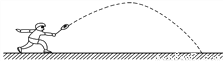
故答案为：k＜1且k≠0． 2013年5月26日，中国羽毛球队蝉联苏迪曼杯团体赛冠军，成就了首个五连冠霸业．比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图)，若不考虑外力因素，羽毛球行进高度y(米)与水平距离x(米)之间满足关系y＝－
x2＋
x＋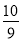
，则羽毛球飞出的水平距离为__________米．
5
【解析】试题解析：当y=0时，0＝，
解得：x1=-1（舍去），x2=5，
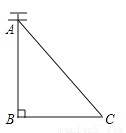
故羽毛球飞出的水平距离为5m． 如图，AC是电线杆AB的一根拉线，测得BC的长为6米，∠ACB=50°，则拉线AC的长为（ ）
A.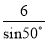 
B.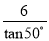 
C. 6cos50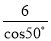° D. 
D
【解析】试题分析：根据Rt△ABC中∠C的余弦值可得：cos50°=，则AC=，故选D．