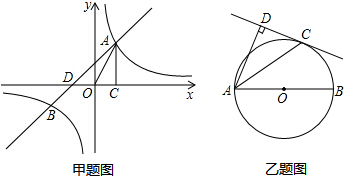
题目内容
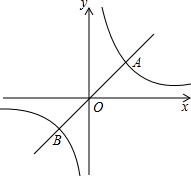 如图,定义:若双曲线y=
如图,定义:若双曲线y=| k |
| x |
| k |
| x |
(1)求双曲线y=
| 1 |
| x |
(2)若双曲线y=
| k |
| x |
| 2 |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)解两个函数的解析式组成的方程组求得交点坐标,过A点作AC⊥x轴于C,;利用勾股定理求得OA的长,则AB即可求解;
(2)△AOC是等腰直角三角形,利用三角函数求得OC和OC的长,则A的坐标可以求得,然后利用待定系数法即可求解.
(2)△AOC是等腰直角三角形,利用三角函数求得OC和OC的长,则A的坐标可以求得,然后利用待定系数法即可求解.
解答: 解:过A点作AC⊥x轴于C,如图,
解:过A点作AC⊥x轴于C,如图,
(1)解方程组
,得
,
,
∴A点坐标为(1,1),B点坐标为(-1,-1),
∴OC=AC=1,∴OA=
,OC=
,∴AB=2OA=2
,
∴双曲线y=
的对径是2
;
(2)∵双曲线的对径为8
,即AB=8
,OA=4
,
∵OA=
OC=
AC,
∴OC=AC=4,
∴点A坐标为(4,4),
把A(4,4)代入双曲线y=
(k>0)得k=16,
即k的值为16.
 解:过A点作AC⊥x轴于C,如图,
解:过A点作AC⊥x轴于C,如图,(1)解方程组
|
|
|
∴A点坐标为(1,1),B点坐标为(-1,-1),
∴OC=AC=1,∴OA=
| 2 |
| 2 |
| 2 |
∴双曲线y=
| 1 |
| x |
| 2 |
(2)∵双曲线的对径为8
| 2 |
| 2 |
| 2 |
∵OA=
| 2 |
| 2 |
∴OC=AC=4,
∴点A坐标为(4,4),
把A(4,4)代入双曲线y=
| k |
| x |
即k的值为16.
点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
世界上最大的动物是蓝鲸,它平均长30米,重达160000千克,其中160000千克用科学记数法表示为( )
| A、1.6×106千克 |
| B、1.6×105千克 |
| C、16×105千克 |
| D、0.16×107千克 |