题目内容
7.已知关于x的方程x2+(2k+1)x+k2-2=0的两个实数根的倒数和等于-$\frac{5}{2}$,求k的值.分析 设方程的两根为x1,x2,根据根与系数的关系得到x1+x2=-(2k+1),x1•x2=k2+2,根据题意得倒数和等于4.即$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=-$\frac{5}{2}$.再把两根关系代入即可.,然后把k=$\frac{5}{2}$或-$\frac{3}{2}$代入原方程利用判别式确定k的值.
解答 解:根据题意,得
x1+x2=-2k-1,x1×x2=k2-2.
∵$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=-$\frac{5}{2}$,
∴$\frac{-2k-1}{{k}^{2}-2}$=-$\frac{5}{2}$,
解得k1=$\frac{5}{2}$,k2=-$\frac{3}{2}$.
当k1=$\frac{5}{2}$,代入方程x2+(2k+1)x+k2-2=0的判别式时,△>0,
k2=-$\frac{3}{2}$,代入方程x2+(2k+1)x+k2-2=0的判别式时,△<0,
∴k=$\frac{5}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了一元二次方程的根的判别式.

练习册系列答案
相关题目
 (1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.
(1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.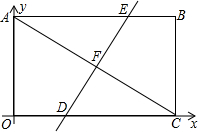 如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4,
如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4,