题目内容
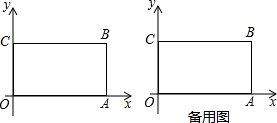
2. 如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.求证:四边形ABCD是矩形.
分析 利用平行线的性质得出∠ADC=90°,再利用勾股定理的逆定理得出∠B=90°,进而得出答案.
解答 证明:四边形ABCD中,AB∥CD,∠BAD=90°,
∴∠ADC=90°,
又∵△ABC中,AB=5,BC=12,AC=13,
满足132=52+122,
∴△ABC是直角三角形,且∠B=90°,
∴四边形ABCD是矩形.
点评 此题主要考查了矩形的判定以及勾股定理的逆定理,正确掌握矩形的判定方法是解题关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
10.分解因式a3-4a的结果是( )
| A. | a(a2-4) | B. | a(a+2)(a-2) | C. | a(a2+2)(a2-2) | D. | a(a2+4)(a2-4) |
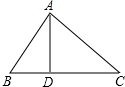 如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高,
如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高, (1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.
(1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4.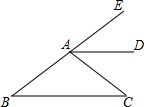 如图,B、A、E三点在同一线上,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC=60°.
如图,B、A、E三点在同一线上,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC=60°.