题目内容
12. 如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )
如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )| A. | 10cm | B. | 9cm | C. | 8cm | D. | 5cm |
分析 由矩形的性质得出AD+DC=10cm,由线段垂直平分线的性质得出CE=CF,由ASA证明△ODE≌△OBF,得出DE=BF,△CDE的周长=DE+CE+DC=BC+DC,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴AB=DC,BC=AD,OA=OC=OB=OD,AD∥BC,
∴∠EDO=∠FBO,.
∵矩形ABCD的周长为20cm,
∴BC+DC=10cm,
∵EF⊥AC,
∴CE=CF,
在△ODE和△OBF中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}&{\;}\\{OD=OB}&{\;}\\{∠DOE=∠BOF}&{\;}\end{array}\right.$,
∴△ODE≌△OBF(ASA),
∴DE=BF,
∴△CDE的周长=DE+CE+DC=BF+CF+DC=BC+DC=10cm.
故选:A.
点评 本题考查了矩形的性质、线段垂直平分线的性质、全等三角形的判定与性质、三角形周长的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
3.下列说法中错误的是( )
| A. | 一个三角形中至少有一个角不少于60° | |
| B. | 三角形的中线不可能在三角形的外部 | |
| C. | 周长相等的两个三角形全等 | |
| D. | 三角形的中线把三角形的面积平均分成相等的两部分 |
7.已知分式$\frac{x-1}{2x}$的值为零,那么x的值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
1. 如图,在平行四边形ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,则OA的取值范围是( )
如图,在平行四边形ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,则OA的取值范围是( )
 如图,在平行四边形ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,则OA的取值范围是( )
如图,在平行四边形ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,则OA的取值范围是( )| A. | 2<OA<5 | B. | 2<OA<8 | C. | 1<OA<4 | D. | 3<OA<8 |
 已知:如图,∠ABE=∠EBC,AE⊥BE,F是AC的中点.求证:EF=$\frac{1}{2}$(BC-AB)
已知:如图,∠ABE=∠EBC,AE⊥BE,F是AC的中点.求证:EF=$\frac{1}{2}$(BC-AB)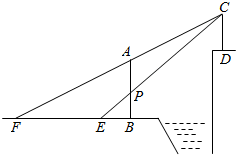 如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,已知:人在塔底B点以西50米的地面E点恰好看到点E、P、C在一直线上,再向西前进150米后从地面F点恰好看到点F、A、C在一直线上,求两铁塔轴线间的距离(即直线AB、CD间的距离)
如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,已知:人在塔底B点以西50米的地面E点恰好看到点E、P、C在一直线上,再向西前进150米后从地面F点恰好看到点F、A、C在一直线上,求两铁塔轴线间的距离(即直线AB、CD间的距离)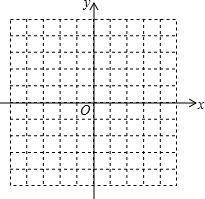 已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3).
已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3). 如图,将△ABC沿BC方向平移至△DEF的位置,若BC=5,BF=15
如图,将△ABC沿BC方向平移至△DEF的位置,若BC=5,BF=15