题目内容
某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件,如果每件涨价1元(售价不可以高于45),那么每星期少卖出10件,设每件涨价x元,每星期销量为y件.
(1)求y关于x的函数关系式(不要求写出自变量x的取值范围);
(2)如何定价才能使每星期的利润为1560元?每星期的销量是多少?
(1)求y关于x的函数关系式(不要求写出自变量x的取值范围);
(2)如何定价才能使每星期的利润为1560元?每星期的销量是多少?
考点:一元二次方程的应用
专题:
分析:(1)依据题意易得出平均每天销售量(y)与涨价x之间的函数关系式为y=150-10x;
(2)一个商品原利润为40-30=10元,每件涨价x元,现在利润为(10+x)元;根据题意,销售量为150-10x,由一个商品的利润×销售量=总利润,列方程求解.
(2)一个商品原利润为40-30=10元,每件涨价x元,现在利润为(10+x)元;根据题意,销售量为150-10x,由一个商品的利润×销售量=总利润,列方程求解.
解答:解:(1)∵如果售价每涨1元,那么每星期少卖10件,
∴每件涨价x元(x为非负整数),每星期销量为:y=150-10x;
(2)设每件涨价x元,依题意得
(10+x)(150-10x)=1560,
解这个方程,得x1=2,x2=3,
∵售价不高于45元,
∴x1=2,x2=3均符合题意,
当x1=2时,每星期的销量是150-10×2=130(件);
当x2=3时,每星期的销量是150-10×3=120(件);
答:该商品每件定价42元或43元才能使每星期的利润为1560元,此时每星期的销量是130件或120件.
∴每件涨价x元(x为非负整数),每星期销量为:y=150-10x;
(2)设每件涨价x元,依题意得
(10+x)(150-10x)=1560,
解这个方程,得x1=2,x2=3,
∵售价不高于45元,
∴x1=2,x2=3均符合题意,
当x1=2时,每星期的销量是150-10×2=130(件);
当x2=3时,每星期的销量是150-10×3=120(件);
答:该商品每件定价42元或43元才能使每星期的利润为1560元,此时每星期的销量是130件或120件.
点评:考查了一元二次方程的应用,提价,实际上就是提高了盈利,而提高了盈利,会带来销售量的下降,列方程时,要注意“一升一降”.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是 某校初三5班50名学生参加全市1分钟跳绳体育考试.1分钟跳绳次数与频数经统计后绘制出下面的频数分布表(60-70表示为大于等于60并且小于70)和扇形统计图.
某校初三5班50名学生参加全市1分钟跳绳体育考试.1分钟跳绳次数与频数经统计后绘制出下面的频数分布表(60-70表示为大于等于60并且小于70)和扇形统计图.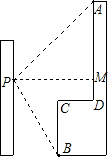 小强在教学楼的点P处观察对面的办公大楼,为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米,求点P到AD的距离(
小强在教学楼的点P处观察对面的办公大楼,为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米,求点P到AD的距离(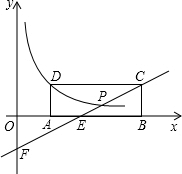 如图,矩形ABCD在第一象限,AB在x轴正半轴上;AB=m,BC=1,直线y=
如图,矩形ABCD在第一象限,AB在x轴正半轴上;AB=m,BC=1,直线y=