题目内容
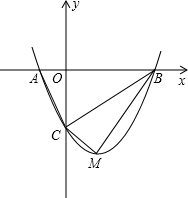 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交与A、B两点,与y轴交与C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交与A、B两点,与y轴交与C点.(1)求抛物线顶点M的坐标(用含m的代数式表示)及A、B两点的坐标;
(2)当m变化时,试证明△BCM与△ABC的面积比值是定值,并求出此定值;
(3)若线段CM的垂直平分线过B点,求抛物线方程.
考点:二次函数综合题
专题:
分析:(1)将抛物线的解析式化为顶点坐标式,即可得到顶点M的坐标;抛物线的解析式中,令y=0,可求得A、B的坐标.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比.
(3)根据线段CM的垂直平分线过B点可以得到CM=CB,利用两点之间的距离公式列出方程求得m的值即可.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比.
(3)根据线段CM的垂直平分线过B点可以得到CM=CB,利用两点之间的距离公式列出方程求得m的值即可.
解答:解:(1)∵y=mx2-2mx-3m=m(x2-2x-3)=m(x-1)2-4m,
∴抛物线顶点M的坐标为(1,-4m);(2分)
∵抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,
∴当y=0时,mx2-2mx-3m=0,
∵m>0,
∴x2-2x-3=0;
解得x1=-1,x2=3,
∴A、B两点的坐标为(-1,0)、(3,0).
(2)当x=0时,y=-3m,
∴点C的坐标为(0,-3m).
∴S△ABC=
|3-(-1)|×|-3m|=6|m|=6m.
过点M作MD⊥x轴于点D,则OD=1,BD=OB-OD=2,
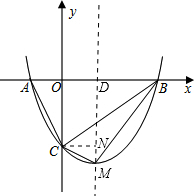 MD=|-4m|=4m.
MD=|-4m|=4m.
∴S△BCM=S△BDM+S梯形OCMD-S△OBC
=
BD•DM+
(OC+OM)•OD-
OB•BC
=
×2×4m+
(3m+4m)×1-
×3×3m
=3m.
∴S△BCM:S△ABC=1:2,
故答案为:
;
(3)∵线段CM的垂直平分线过B点,
∴BM=BC,
∵抛物线y=mx2-2mx-3m(m>0)的顶点M的坐标为(1,-4m),B(3,0),C(0,-3m),
∴32+(3m)2=(3-1)2-(4m)2,
解得:m=
.
故解析式为:y=
x2-
x-
.
∴抛物线顶点M的坐标为(1,-4m);(2分)
∵抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,
∴当y=0时,mx2-2mx-3m=0,
∵m>0,
∴x2-2x-3=0;
解得x1=-1,x2=3,
∴A、B两点的坐标为(-1,0)、(3,0).
(2)当x=0时,y=-3m,
∴点C的坐标为(0,-3m).
∴S△ABC=
| 1 |
| 2 |
过点M作MD⊥x轴于点D,则OD=1,BD=OB-OD=2,
 MD=|-4m|=4m.
MD=|-4m|=4m.∴S△BCM=S△BDM+S梯形OCMD-S△OBC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=3m.
∴S△BCM:S△ABC=1:2,
故答案为:
| 1 |
| 2 |
(3)∵线段CM的垂直平分线过B点,
∴BM=BC,
∵抛物线y=mx2-2mx-3m(m>0)的顶点M的坐标为(1,-4m),B(3,0),C(0,-3m),
∴32+(3m)2=(3-1)2-(4m)2,
解得:m=
| ||
| 7 |
故解析式为:y=
| ||
| 7 |
2
| ||
| 7 |
3
| ||
| 7 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
 如图,已知函数y=
如图,已知函数y= 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上两点,经过点A、C、B的抛物线的一部分了C1经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,已知点C的坐标为(0,-1.5),M是抛物线C2;y=tx2-2tx-3t(t<0)的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上两点,经过点A、C、B的抛物线的一部分了C1经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,已知点C的坐标为(0,-1.5),M是抛物线C2;y=tx2-2tx-3t(t<0)的顶点. 为了倡导“节约用水,从我做起”的活动,某市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”的活动,某市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图. 如图,在菱形ABCD中,AB:AC=m:n,点P为BC边上一点,以AP为对角线作菱形AFPM,满足∠ABC=∠AFP,连结BF,猜想BF与CP的数量关系,并证明你的结论.
如图,在菱形ABCD中,AB:AC=m:n,点P为BC边上一点,以AP为对角线作菱形AFPM,满足∠ABC=∠AFP,连结BF,猜想BF与CP的数量关系,并证明你的结论.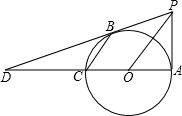 如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D.
如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D. 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是 某校初三5班50名学生参加全市1分钟跳绳体育考试.1分钟跳绳次数与频数经统计后绘制出下面的频数分布表(60-70表示为大于等于60并且小于70)和扇形统计图.
某校初三5班50名学生参加全市1分钟跳绳体育考试.1分钟跳绳次数与频数经统计后绘制出下面的频数分布表(60-70表示为大于等于60并且小于70)和扇形统计图.