题目内容
如图，在△ABC中AB=AC，∠A=56°，BD⊥AC于D，求∠CBD的度数．考点：等腰三角形的性质
专题：
分析：先根据已知求得两底角的度数，再根据三角形内角和定理即可求得∠DBC的度数．
解答：解：∵AB=AC，∠A=56°，
∴∠ABC=∠ACB=62°．
∵BD⊥AC于D，
∴∠CBD=90°-62°=28°．
∴∠ABC=∠ACB=62°．
∵BD⊥AC于D，
∴∠CBD=90°-62°=28°．
点评：本题主要考查等腰三角形的性质，解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题，此题难度一般．
练习册系列答案
相关题目
用长8米的铝材制成一个矩形窗框，使它的面积为5平方米．若设它的一边长为x米，根据题意列出关于x的方程为（ ）
| A、x（8-x）=5 |
| B、x（4+x）=5 |
| C、x（4-x）=5 |
| D、x（8-2x）=5 |
如图，已知函数y=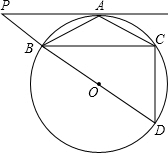
已知：如图⊙O是△ABC的外接圆，P为圆外一点，PA∥BC，且A为劣弧
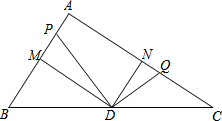如图，在Rt△ABC中，∠A=90°，AB=6，AC=8，点M、N分别为AB，AC边的中点，点D为BC边的中点，动点P从点A出发，沿射线AB方向移动，作∠PDQ=90°，点Q在AC上，设AP=x，CQ=y．
如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上两点，经过点A、C、B的抛物线的一部分了C1经过点A、D、B的抛物线的一部分C2组成一条封闭曲线，已知点C的坐标为（0，-1.5），M是抛物线C2；y=tx2-2tx-3t（t＜0）的顶点．
为了倡导“节约用水，从我做起”的活动，某市政府决定对市直机关500户家庭的用水情况作一次调查，调查小组随机抽查了其中100户家庭一年的月平均用水量（单位：吨）．并将调查结果制成了如图所示的条形统计图．
如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，则∠COD的度数是