Question

19．如图，在△ABC中，AB=AC，以AB为半径的⊙O交AC于点E，交BC于点D，过点D作⊙O的切线DF，交AC于点F．
（1）求证：DF⊥AC；
（2）若CE=2，CD=3，求AB的长；
（3）若⊙O的半径为4，∠CDF=22.5°，求阴影部分的面积．

Answer 1

分析 （1）利用圆周角定理得出AD⊥BC，再利用三角形中位线的判定与性质得出OD∥AC，进而得出DF⊥OD，进而得出DF⊥AC；
（2）首先证明△ACD∽△BCE，再利用相似三角形的性质得出AC的长，进而得出答案；
（3）利用S_阴影=S_扇形AOE-S_△AOE进而求出答案．

解答 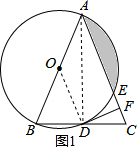（1）证明：如图1，连接AD、OD
∵AB为⊙O的直径，
∴AD⊥BC，
又∵AB=AC，
∴点D是BC的中点，
∵点O是AB的中点，
∴OD是△ABC的中位线，OD∥AC，
∵DF是⊙O的切线，OD是过切点的半径，
∴DF⊥OD，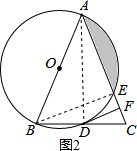
∴DF⊥AC；

（2）解：如图2，连接BE
∵AB为⊙的直径，
∴BE⊥AC，
又∵AD⊥BC，
∴∠ADC=∠BEC=90°，
而∠C=∠C，
∴△ACD∽△BCE，
∴$\frac{CD}{CE}$=$\frac{AC}{BC}$，
∴$\frac{3}{2}$=$\frac{AC}{6}$，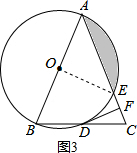
解得：AC=9，
∴AB=AC=9；

（3）解：如图3，连接OE，
在Rt△CDF中，∵∠CDF=22.5°，∴∠C=67.5°，
∴∠ABC=∠C=67.5°，∠A=45°，
∵OA=OE，
∴∠AOE=90°，
∴S_阴影=S_扇形AOE-S_△AOE=$\frac{90π×{4}^{2}}{360}$-$\frac{1}{2}$×4×4=4π-4．

点评 此题主要考查了切线的性质以及扇形面积求法以及相似三角形的判定与性质等知识，正确得出△ACD∽△BCE是解决问题（2）的关键．