题目内容
9.观察下面的运算:(1)(2$\sqrt{3}$$+\sqrt{2}$)(2$\sqrt{3}$-$\sqrt{2}$)=(2$\sqrt{3}$)2-($\sqrt{2}$)2=12-2=10;
(2)(a$\sqrt{x}$+b$\sqrt{y}$)(a$\sqrt{x}$-b$\sqrt{y}$)=(a$\sqrt{x}$)2-(b$\sqrt{y}$)2=a2x-b2y(x,y≥0).
可以看出,若一个式子(a$\sqrt{x}$+b$\sqrt{y}$)乘以另一个式子(a$\sqrt{x}$-b$\sqrt{y}$),其积是有理式,其中的一个式子叫做另一个式子的有理化因式.
试求:(1)4$\sqrt{3}$-3$\sqrt{2}$的有理化因式;(2)4$\sqrt{x}$+2$\sqrt{y}$(x,y≥0)的有理化因式.
分析 (1)根据平方差公式,可得有理化因式;
(2)根据平方差公式,可得有理化因式.
解答 解:(1)(4$\sqrt{3}$-3$\sqrt{2}$)(4$\sqrt{3}$+3$\sqrt{2}$)=(4$\sqrt{3}$)2-(3$\sqrt{2}$)2=48-18=30,
4$\sqrt{3}$-3$\sqrt{2}$的有理化因式4$\sqrt{3}$+3$\sqrt{2}$;
(2)(4$\sqrt{x}$+2$\sqrt{y}$)(4$\sqrt{x}$-2$\sqrt{y}$)=(4$\sqrt{x}$)2-(2$\sqrt{y}$)2=16x-4y,
4$\sqrt{x}$+2$\sqrt{y}$(x,y≥0)的有理化因式4$\sqrt{x}$-2$\sqrt{y}$(x,y≥0).
点评 本题考查了分母有理化,利用平方差公式是解题关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,在△ABC中,AB=AC,以AB为半径的⊙O交AC于点E,交BC于点D,过点D作⊙O的切线DF,交AC于点F.
如图,在△ABC中,AB=AC,以AB为半径的⊙O交AC于点E,交BC于点D,过点D作⊙O的切线DF,交AC于点F.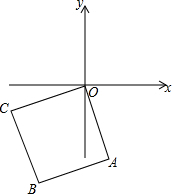 已知正方形OABC在直角坐标系中(如图),A(1,-3),求点B、C的坐标.
已知正方形OABC在直角坐标系中(如图),A(1,-3),求点B、C的坐标.