题目内容
7.在平面内,先将一个多边形以点O为位似中心放大或缩小,使得新多边形与原多边形对应线段的比为k,并且原多边形上的任意一点P的对应点P1在线段OP或其延长线上:接着将所得多边形以O为旋转中心,逆时针旋转一个角度θ,这种经过放缩和旋转的图形变换叫做旋转相似变换,记为O(k,θ),其中O叫做旋转相似中心,k叫做相似比,θ叫做旋转角.现将直角边长为1的等腰直角三角形ABC(∠C=90°)作旋相似变换B(2,60°),若点A的对应点为D,则线段AD的长为$\sqrt{6}$.分析 根据题意画出图形,求出BD的长,根据余弦定理求出AD.
解答 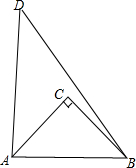 解:如图,∵等腰直角三角形ABC的直角边长为1,
解:如图,∵等腰直角三角形ABC的直角边长为1,
∴BA=$\sqrt{2}$,
则BD=2$\sqrt{2}$,
∵∠ABD=60°,
∴AD2=AB2+BD2-2×AB×BD×cos60°=6,
∴AD=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题主要考查的是位似变换的定义和性质以及旋转相似变换的定义,解答该题的关键是弄清楚O(k,θ)所表达的含义,其中点0叫做旋转相似中心,k叫做相似比,θ叫做旋转角,注意余弦定理的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.多项式5mx3+25mx2-10mxy各项的公因式是( )
| A. | 5mx2 | B. | 5mxy | C. | mx | D. | 5mx |
16.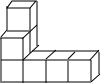 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )
 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )| A. | 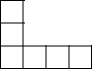 | B. | 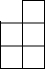 | C. |  | D. |  |
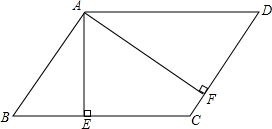 如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D.
如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D. 如图,在?ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为36°.
如图,在?ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为36°. 如图,在?ABCD中,AB=$\frac{1}{2}$AD,AB=AE=BF,试探寻CE与DF的位置关系.
如图,在?ABCD中,AB=$\frac{1}{2}$AD,AB=AE=BF,试探寻CE与DF的位置关系.