题目内容
14.已知:$\sqrt{{x}^{2}+25}$-$\sqrt{{x}^{2}-15}$=4,求$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$的值.分析 首先把$\sqrt{{x}^{2}+25}$-$\sqrt{{x}^{2}-15}$=4,两边同乘$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$的数值,再进一步求得($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$)的数值即可.
解答 解:∵$\sqrt{{x}^{2}+25}$-$\sqrt{{x}^{2}-15}$=4,
∴($\sqrt{{x}^{2}+25}$-$\sqrt{{x}^{2}-15}$)($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$)=4($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$),
∴4($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$)=40,
∴$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$=10.
点评 此题考查二次根式的化简求值,注意式子的特点,灵活运用平方差公式解决问题,注意整体思想的渗透.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.某商品经过两次降价,零售价降为原来的$\frac{1}{2}$,已知两次降价的百分率均为x,则列出方程正确的是( )
| A. | ${(1+x)^2}=\frac{1}{2}$ | B. | ${(1-x)^2}=\frac{1}{2}$ | C. | (1+x)2=2 | D. | (1-x)2=2 |
3.以下不能构成三角形边长的数组是( )
| A. | 1,$\sqrt{5}$,2 | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 3,4,5 | D. | 32,42,52 |
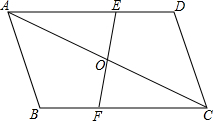 如图,在?ABCD中,过AC中点O作直线分别交AD、BC于点E、F.求证:OE=OF.
如图,在?ABCD中,过AC中点O作直线分别交AD、BC于点E、F.求证:OE=OF.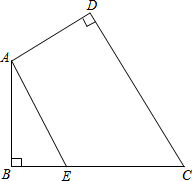 如图,四边形ABCD中,∠D=∠B=90°,∠AEC=∠BAD,求证:AE∥DC.
如图,四边形ABCD中,∠D=∠B=90°,∠AEC=∠BAD,求证:AE∥DC.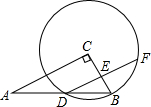 如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,弦DF∥AC,则DF的长为5$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,弦DF∥AC,则DF的长为5$\sqrt{3}$.