题目内容
9．
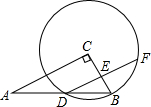如图，在Rt△ABC中，∠C=90°，AB=10，若以点C为圆心，CB长为半径的圆恰好经过AB的中点D，弦DF∥AC，则DF的长为5$\sqrt{3}$．
分析 连接CD，则CD=BC，再由点D是AB的中点可知CD=BD，△BCD是等边三角形，由∠C=90°，DF∥AC可知BC⊥DF，故点E是BC的中点，再根据勾股定理求出DE的长，进而可得出结论．
解答 
解：连接CD，则CD=BC，
∵点D是AB的中点，
∴CD=BD=$\frac{1}{2}$AB=5，
∴△BCD是等边三角形．
∵∠C=90°，DF∥AC，
∴BC⊥DF，
∴点E是BC的中点，
∴BC=$\frac{5}{2}$，
∴DE=$\sqrt{{CD}^{2}-{CE}^{2}}$=$\sqrt{{5}^{2}-{（\frac{5}{2}）}^{2}}$=$\frac{5\sqrt{3}}{2}$，
∴DF=2DE=5$\sqrt{3}$．
故答案为：5$\sqrt{3}$．
点评 本题考查的是垂径定理，根据直角三角形及等边三角形的性质是解答此题的关键．
练习册系列答案
相关题目
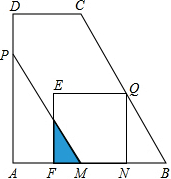如图，在梯形ABCD中，AB∥CD，∠A=90°，AB=AD=10，CD=5，动点P从点A出发，沿折线AD-DC以每秒4个单位的速度向点C运动；点Q从点B出发，沿线段BC以每秒$\sqrt{5}$个单位的速度向点C运动，P，Q两点同时出发，当其中一点到达终点时，另一点也停止运动，过点P作PM∥BC交AB于M，过点Q作QN⊥AB交AB于N，以线段QN为一边在QN的左侧作正方形QEFN，设运动时间为t（s），线段PM扫过平面部分与正方形QEFN重叠部分的面积为S．
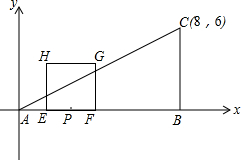在Rt△ABC中，∠ABC=90°，以A为坐标原点，AB所在直线为x轴，建立平面直角坐标，且C坐标（8，6），点P在AB上，AP=2，E、F同时从点P出发，分别沿PA、PB以每秒1个单位的速度向A、B匀速运动，点E到达A后立即以原速沿AB向B运动，点E再次返回点P停止，点F也随之停止运动，在点E、F运动过程中，以EF为边向上做正方形EFGH，设E、F运动的时间为t秒（t＞0），正方形EFGH与△ABC重叠面积为S．
