题目内容
3．以下不能构成三角形边长的数组是（ ）| A． | 1，$\sqrt{5}$，2 | B． | $\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$ | C． | 3，4，5 | D． | 32，42，52 |
分析 根据三角形的三边关系，只要两条较小的边的和大于最大的边即可构成三角形，反之不能构成三角形．
解答 解：解：根据三角形的三边关系，得
A、1+2＞$\sqrt{5}$，可以构成三角形，故选项错误；
B、$\sqrt{3}+\sqrt{4}＞\sqrt{5}$，可以构成三角形，故选项错误；
C、3+4＞5，可以构成三角形，故选项错误；
D、32+42=52，不可以构成三角形，故选项正确．
故选D．
点评 本题主要考查了三角形的三边关系定理：任意两边之和大于第三边．只要满足两短边的和大于最长的边，就可以构成三角形．
练习册系列答案
考前必练系列答案
相关题目
13．若$\sqrt{（2x-3）^{2}}$=3-2x，则x的取值范围是（ ）
| A． | x≥$\frac{3}{2}$ | B． | x＞$\frac{3}{2}$ | C． | x≤$\frac{3}{2}$ | D． | x＜$\frac{3}{2}$ |
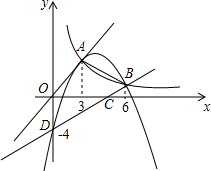如图，在平面直角坐标系中，正比例函数y=x和反比例函数y=$\frac{9}{x}$的图象交于第一象限内点A