题目内容

10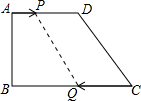．直角梯形ABCD中，∠B=90°，AD∥BC，AD=18cm，BC=21cm，点P从点A以1cm/s的速度向点D运动，同时点Q从点C以2cm/s的速度向点B运动．问：
（1）当运动时间t为何值时，四边形PQCD 是平行四边形．
（2）当运动时间t为何值时，四边形ABQP是矩形．（可自己作图完成）

分析 （1）根据题意可得PA=t，CQ=2t，则PD=AD-PA=18-t，当PD=CQ时，四边形PQCD为平行四边形，可得方程18-t=2t，解此方程即可求得答案；
（2）首先过P作PQ⊥BC于Q，由当AP=BQ时，四边形ABQP是矩形，即t=21-2t时，解此方程即可求得答案．

解答 解：（1）根据题意得：PA=t，CQ=2t，则PD=AD-PA=18-t，
∵AD∥BC，
∴PD∥CQ，
∴当PD=CQ时，四边形PQCD为平行四边形，
即18-t=2t，
解得：t=6，
即当t=6时，四边形PQCD为平行四边形；
（2）过P作PQ⊥BC于Q，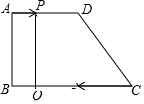
则四边形ABQP是矩形，
∴AP=BQ，
即t=21-2t，
解得：t=7，

点评 此题考查了直角梯形的性质、平行四边形的判定、等腰梯形的判定以及全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想与方程思想的应用．

练习册系列答案
相关题目
1．如图，在平面直角坐标系中，已知点A（-5，0），B（5，0），D（2，7），连接AD交y轴于C点．
（1）求C点的坐标；
（2）动点P从B点出发以每秒1个单位的速度沿BA方向运动，同时动点Q从C点出发也以每秒1个单位的速度沿y轴正半轴方向运动（当P点运动到A点时，两点都停止运动）．设从出发起运动了x秒．                  
①请用含x的代数式分别表示P，Q两点的坐标；
②当x=2时，y轴上是否存在一点E，使得△AQE的面积与△APQ的面积相等？若存在，求E的坐标；若不存在，说明理由．
1．如图，点E是等边△ABC内一点，连按BE、AE，且AE=BE，将线段BC沿BE翻折，使点C落在点D处，连接DE．下列结论正确的个数为（　　）
①∠ACB=2∠BDE；②∠AEB=90°；③AC=BD；④AC⊥BD．
A．1个B．2个C．3个D．4个
18．如图，AB⊥BC，射线CM⊥BC，且BC=5，AB=1，点P是线段BC （不与点B、C重合）上的动点，过点P作DP⊥AP交射线CM于点D，连结AD．
（1）如图1，若BP=4，求△ABP的周长．
（2）如图2，若DP平分∠ADC，试猜测PB和PC的数量关系，并说明理由．
（3）若△PDC是等腰三角形，作点B关于AP的对称点B′，连结B′D，则B′D=5．（请直接写出答案）
5．下列各式正确的是（　　）
A．$\sqrt{81}$=±9B．|3.14-π|=π-3.14C．$\sqrt{-27}$=-9$\sqrt{3}$D．$\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$
15．如图，Rt△ABC内接于⊙O，点E为弧BC中点，AD平分∠BAC交BC于D，连接AD、DE．
（1）求证：∠ADB=∠CDE；
（2）AC交DE于H，且∠DHC=90°，连接BE分别交AD、AC于M、N，求证：BM=EN．
（3）在（1）的条件下，连接BE交AD于M，连接CM交DE于K，若CM⊥DE，若BD=2$\sqrt{10}$，求AM的长．
2．如图，在△ABC中，点D、E分别在AB、AC上，且DE∥BC，则下列结论错误的是（　　）
A．$\frac{BD}{AB}=\frac{EC}{AC}$B．$\frac{AD}{DB}=\frac{AE}{EC}$C．$\frac{AD}{AB}=\frac{AE}{AC}$D．$\frac{AD}{DB}=\frac{DE}{BC}$

一个圆锥的高为3，侧面展开图是半圆，则圆锥的侧面积是_________
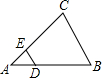17．如图，在△ABC中，DE∥BC，DB=2AD，△ADE的面积为1，则四边形DBCE的面积为（　　）
A．2B．5C．6D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网