题目内容
2.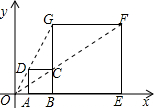 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2).
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2).
分析 先利用位似的性质得到$\frac{BC}{6}$=$\frac{OB}{OB+6}$=$\frac{1}{3}$,然后利用比例性质求出BC和OB即可得到C点坐标.
解答 解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.
∴$\frac{BC}{EF}$=$\frac{OB}{OE}$=$\frac{1}{3}$,
而BE=EF=6,
∴$\frac{BC}{6}$=$\frac{OB}{OB+6}$=$\frac{1}{3}$,
∴BC=2,OB=3,
∴C(3,2).
故答案为(3,2)
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列说法正确的是( )
| A. | 两个矩形一定相似 | B. | 两个菱形一定相似 | ||
| C. | 两个等腰三角形一定相似 | D. | 两个等边三角形一定相似 |
14.下列各数中,为负数的是( )
| A. | -1 | B. | 0 | C. | 2 | D. | 3.14 |
11.下列二次函数的图象中,开口最大的是( )
| A. | y=x2 | B. | y=2x2 | C. | y=$\frac{1}{100}$x2 | D. | y=-x2 |
10.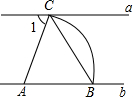 如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
 如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )| A. | 36° | B. | 54° | C. | 72° | D. | 63° |

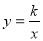 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
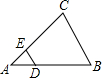 如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )