Question

18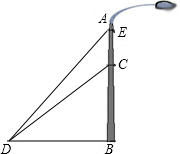．如图，一垂直于地面的灯柱AB被一钢线CD固定，CD与地面成45°夹角（∠CDB=45°），在C点上方2米处加固另一条钢线ED，ED与地面成53°夹角（∠EDB=53°），那么钢线ED的长度约为多少米？（结果精确到1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

Answer 1

分析 根据题意，可以得到BC=BD，由∠CDB=45°，∠EDB=53°，由三角函数值可以求得BD的长，从而可以求得DE的长．

解答 解：设BD=x米，则BC=x米，BE=（x+2）米，
在Rt△BDE中，tan∠EDB=$\frac{BE}{DB}=\frac{x+2}{x}$，
即$\frac{x+2}{x}≈1.33$，
解得，x≈6.06，
∵sin∠EDB=$\frac{BE}{ED}$，
即0.8=$\frac{8.06}{ED}$，
解得，ED≈10
即钢线ED的长度约为10米．

点评 本题考查解直角三角形的应用，解题的关键是明确题意，利用三角函数值求出相应的边的长度．