题目内容
8.不改变分式的值,使分式的分子、分母中最高次项的系数为正数,则$\frac{3-x}{{x}^{2}+1}$=-$\frac{x-3}{{x}^{2}+1}$.分析 根据分式的分子、分母、分式改变其中任何两项的符号,分式的值不变.
解答 解:$\frac{3-x}{{x}^{2}+1}$=-$\frac{x-3}{{x}^{2}+1}$,
故答案为:-$\frac{x-3}{{x}^{2}+1}$.
点评 本题考查了分式的基本性质,注意分式的分子、分母、分式改变其中任何两项的符号,分式的值不变.

练习册系列答案
相关题目
13.下列各式不是一元一次不等式组的是( )
| A. | $\left\{\begin{array}{l}{x>3}\\{x<1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x<5}\\{2x-1<9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-1>3}\\{y+2<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-1>3}\\{x-3<2}\\{2x-1<5}\end{array}\right.$ |
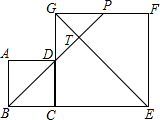 如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.
如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.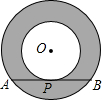 如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )
如图,半径均为整数的同心圆组成的“圆环带”,若大圆的弦AB与小圆相切于点P,且弦AB的长度为定值$4\sqrt{3}$,则满足条件的不全等的“圆环带”有( )
 在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABC的周长是17cm,AC=5cm,△ABD的周长是12cm.
在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABC的周长是17cm,AC=5cm,△ABD的周长是12cm. 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.
为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.