题目内容
18.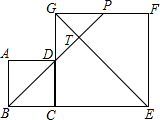 如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.
如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为4$\sqrt{2}$.
分析 根据正方形的对角线平分一组对角可得∠ADB=∠CGE=45°,再求出∠GDT=45°,从而得到△DGT是等腰直角三角形,根据正方形的边长求出DG,再根据等腰直角三角形的直角边等于斜边的$\frac{\sqrt{2}}{2}$倍求解即可.
解答 解:∵BD、GE分别是正方形ABCD,正方形CEFG的对角线,
∴∠ADB=∠CGE=45°,
∴∠GDT=180°-90°-45°=45°,
∴∠DTG=180°-∠GDT-∠CGE=180°-45°-45°=90°,
∴△DGT是等腰直角三角形,
∵两正方形的边长分别为3,5,
∴GE=$\sqrt{{5}^{2}-{3}^{2}}=4$,DG=5-3=2,
∴GT=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
∴ET=$4\sqrt{2}$,
故答案为:4$\sqrt{2}$.
点评 本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等腰直角三角形的判定与性质.

练习册系列答案
相关题目
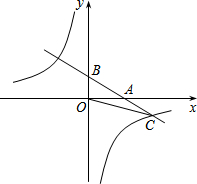 如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为$\sqrt{3}$.
如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为$\sqrt{3}$.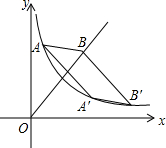 如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,设点B的横坐标为m,试用m的式子表示出点B′的坐标,并求出m的值.
如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,设点B的横坐标为m,试用m的式子表示出点B′的坐标,并求出m的值.