题目内容
19. E、F在菱形ABCD的边AB和BC上,DE=DF=AD,且∠EDF=30°,则∠BEF=35°.
E、F在菱形ABCD的边AB和BC上,DE=DF=AD,且∠EDF=30°,则∠BEF=35°.
分析 由菱形的性质得出AB=BC=CD=AD,∠A=∠C,AD∥BC,证出AD=DE=DF=CD,与等腰三角形的性质得出∠DEF=∠EFD=75°,∠A=∠DEA,∠C=∠DFC,得出∠A=∠DEA=∠C=∠DFC,由AAS证明△DAE≌△DCF,得出AE=CF,证出BE=BF,得出∠BEF=∠BFE,设∠BEF=∠BFE=x,∴∠EBF=180°-2x,∠A=∠DEA=180°-∠DEF-∠BEF=105°-x,由平行线的性质得出105°-x+180°-2x=180°,解方程即可.
解答 解:∵四边形ABCD为菱形,
∴AB=BC=CD=AD,∠A=∠C,AD∥BC,
∵DE=DF=AD,∠EDF=30°,
∴AD=DE=DF=CD,∠DEF=∠EFD=75°,
∴∠A=∠DEA,∠C=∠DFC,
∴∠A=∠DEA=∠C=∠DFC,
在△DAE和△DCF中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{∠DEA=∠DFC}&{\;}\\{AD=CD}&{\;}\end{array}\right.$,
∴△DAE≌△DCF(AAS),
∴AE=CF,
∴BE=BF,
∴∠BEF=∠BFE,
设∠BEF=∠BFE=x,
∴∠EBF=180°-2x,∠A=∠DEA=180°-∠DEF-∠BEF=105°-x,
∵AD∥BC,
∴∠A+∠EBF=180°,
∴105°-x+180°-2x=180°,
解得:x=35°;
故答案为:35°.
点评 本题考查了菱形的性质、等腰三角形的性质、全等三角形的判定与性质、三角形内角和定理等知识;熟练掌握菱形的性质和等腰三角形的性质是解决问题的关键.

练习册系列答案
相关题目
9.下列运算正确的是( )
| A. | 2a3•a4=2a7 | B. | a3+a4=a7 | C. | (2a4)3=8a7 | D. | a3÷a4=a |
10.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列图形:任取一个既是轴对称图形又是中心对称图形的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
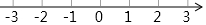 解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{3x+1>-2}\\{\frac{x}{2}≥x-1}\end{array}\right.$,并将其解集在数轴上表示出来.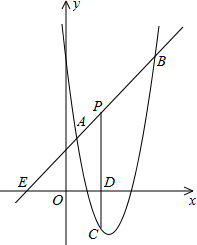 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.