题目内容
5．若方程mx-2y=4的一个解是$\left\{\begin{array}{l}{x=6}\\{y=12}\end{array}\right.$，则m=$\frac{14}{3}$．分析 直接把x=6，y=12代入方程mx-2y=4，求出m的值即可．
解答 解：∵方程mx-2y=4的一个解是$\left\{\begin{array}{l}{x=6}\\{y=12}\end{array}\right.$，
∴6m-24=4，解得，m=$\frac{14}{3}$．
故答案为：$\frac{14}{3}$．
点评 本题考查的是二元一次方程的解，在二元一次方程中，任意给出一个未知数的值，总能求出另一个未知数的一个唯一确定的值，所以二元一次方程有无数解．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
15．已知一个反比例函数的图象经过点A（3，-4），那么不在这个函数图象上的点是（ ）
| A． | （-3，-4） | B． | （-3，4） | C． | （2，-6） | D． | （$\frac{\sqrt{2}}{2}$，-12$\sqrt{2}$） |
12．
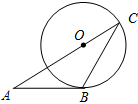如图，AB与⊙O目切于点B，连接AO，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C的度数为（ ）
如图，AB与⊙O目切于点B，连接AO，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C的度数为（ ）| A． | 50° | B． | 25° | C． | 20° | D． | 15° |
19．
已知实数m、n在数轴上的对应点的位置如图，则|m-n|+$\sqrt{1-2n+{n}^{2}}$=（ ）
已知实数m、n在数轴上的对应点的位置如图，则|m-n|+$\sqrt{1-2n+{n}^{2}}$=（ ）| A． | m-1 | B． | m+1 | C． | 2n-m+1 | D． | 2n-m-1 |
如图，下面的几何体由两个大小相同的正方体和一个圆柱体组成，则它的左视图是（ ）
