题目内容
18．
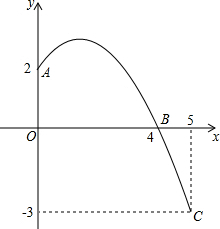已知：如图是抛物线y=ax2+bx+c（a≠0）的一部分，且图象经过A，B，C三点，求抛物线的解析式．
分析 将A、B、C三点分别代入一般式y=ax2+bx+c，然后解方程组即可求得解析式．
解答 解：因为y=ax2+bx+c的图象经过A（0，2），C（4，0），B（5，-3）三点，
∴$\left\{\begin{array}{l}{c=2}\\{16a+4b+c=0}\\{25a+5b+c=-3}\end{array}\right.$，
解得：a=-$\frac{1}{2}$，b=$\frac{3}{2}$，c=2．
因此这个二次函数的解析式是 y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2．
点评 此题主要考查了待定系数法求二次函数解析式和二次函数图象的知识点，熟练掌握待定系数法是解题的关键．
练习册系列答案
相关题目
8．已知三个有理数a，b，c的积是正数，它们的和是负数，当x=$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}$时，求代数式：-3x19-2008x-2013的值．
6．
如图，抛物线顶点坐标是P（1，2），函数y随自变量x的增大而减小的x的取值范围是（ ）
如图，抛物线顶点坐标是P（1，2），函数y随自变量x的增大而减小的x的取值范围是（ ）| A． | x＞2 | B． | x＜2 | C． | x＞1 | D． | x＜1 |
6．下列各组条件中，能判定△ABC≌△DEF的是（ ）
| A． | AB=DE，BC=EF，∠A=∠D | B． | ∠A=∠D，∠C=∠F，AC=EF | ||
| C． | AB=DE，BC=EF，AC=DF | D． | ∠B=∠E |
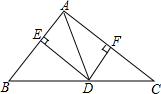如图，在△ABC中，AB=3cm，AC=4cm，AD是BC的中线，DE，DF分别是△ABD和△ACD的高，求DE：DF的值．