题目内容
若用圆心角为90°,面积为16π的扇形卷成一个无底圆锥形桶,则这个圆锥形桶的高为 .
考点:圆锥的计算
专题:计算题
分析:设扇形的半径为R,圆锥的底面圆的半径为r,先根据扇形的面积公式得16π=
,解得R=8,再利用弧长公式得到2πr=
,解得r=2,然后利用勾股定理计算这个圆锥形桶的高.
| 90•π•R2 |
| 360 |
| 90•π•8 |
| 180 |
解答:解:设扇形的半径为R,圆锥的底面圆的半径为r,
根据题意得16π=
,解得R=8,
2πr=
,解得r=2,
所以个圆锥形桶的高=
=2
.
故答案为2
.
根据题意得16π=
| 90•π•R2 |
| 360 |
2πr=
| 90•π•8 |
| 180 |
所以个圆锥形桶的高=
| 82-22 |
| 15 |
故答案为2
| 15 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在分别标有号码2、3、4、…10的9个球中,随机取出两个球,记下它们的标号,则较大标号被较小标号整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
当a=-2时,下列多项式的值为正数的是( )
| A、-a-4 |
| B、-3+a2 |
| C、2a-1 |
| D、a2-4 |
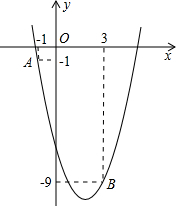 如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
如图,已知二次函数y=ax2-4x+c的图象经过点A和点B. 已知:如图,在Rt△ABC中,∠C=90°,DC=1.点D为BC边上一点,且BD=2AD,∠DAC=30°,求斜边AB长(结果保留根号).
已知:如图,在Rt△ABC中,∠C=90°,DC=1.点D为BC边上一点,且BD=2AD,∠DAC=30°,求斜边AB长(结果保留根号).