题目内容
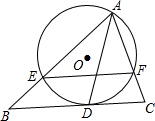 如图,直线BC与半径为2的⊙O相切于点D,A是⊙O上一点,AB交⊙O于点E,AC交⊙O于点F,BC∥EF.
如图,直线BC与半径为2的⊙O相切于点D,A是⊙O上一点,AB交⊙O于点E,AC交⊙O于点F,BC∥EF.(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,求EF的长.
考点:切线的性质
专题:
分析:(1)如图,连接OD.利用切线的性质、垂径定理以及圆周角、弧、弦间的关系证得结论;
(2)连接OE.由三角函数和垂径定理可将EF的长求出.
(2)连接OE.由三角函数和垂径定理可将EF的长求出.
解答: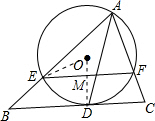 (1)证明:如图,连接OD交EF于点M.
(1)证明:如图,连接OD交EF于点M.
∵直线BC与⊙O相切于点D,
∴OD⊥BC,
又BC∥EF,
∴OD⊥EF,
∴EM=FM.
∴
=
,
∴∠EAD=∠FAD,即AD平分∠BAC;
(2)解:连接OE.由(1)知,AD平分∠BAC,OD⊥EF.
∵∠BAC=60°,
∴∠EAD=30°
∴∠EOD=2∠EAD=60°,
∴∠COE=60°.
在Rt△EOM中,EM=sin60°×OE=
×2=
,
∵EF=2EM,
∴EF=2
.
 (1)证明:如图,连接OD交EF于点M.
(1)证明:如图,连接OD交EF于点M.∵直线BC与⊙O相切于点D,
∴OD⊥BC,
又BC∥EF,
∴OD⊥EF,
∴EM=FM.
∴
 |
| ED |
 |
| FD |
∴∠EAD=∠FAD,即AD平分∠BAC;
(2)解:连接OE.由(1)知,AD平分∠BAC,OD⊥EF.
∵∠BAC=60°,
∴∠EAD=30°
∴∠EOD=2∠EAD=60°,
∴∠COE=60°.
在Rt△EOM中,EM=sin60°×OE=
| ||
| 2 |
| 3 |
∵EF=2EM,
∴EF=2
| 3 |
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
在分别标有号码2、3、4、…10的9个球中,随机取出两个球,记下它们的标号,则较大标号被较小标号整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知△ABC,
已知△ABC,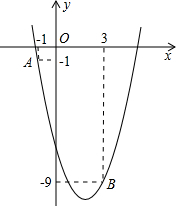 如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.