题目内容
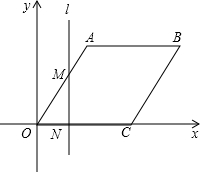 如图,在平面直角坐标系中,OA∥CB,AB∥OC,∠AOC=60°,OC=OA=4;
如图,在平面直角坐标系中,OA∥CB,AB∥OC,∠AOC=60°,OC=OA=4;(1)求A、B两点的坐标;
(2)垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M、N(点M在点N的上方).设△OMN的面积为S,直线l运动时间为t秒(0≤t≤6),试求S与t的函数表达式.
考点:四边形综合题
专题:
分析:(1)根据已知可得四边形OABC为菱形,然后根据菱形性质得出OA=AB=BC=CO=4,过A作AD⊥OC于D,求出AD、OD,即可得出答案;
(2)有三种情况:①当0≤t≤2时,直线l与OA、OC两边相交,②当2<t≤4时,直线l与AB、OC两边相交,③当4<t≤6时,直线l与AB、BC两边相交,画出图形求出即可;
(2)有三种情况:①当0≤t≤2时,直线l与OA、OC两边相交,②当2<t≤4时,直线l与AB、OC两边相交,③当4<t≤6时,直线l与AB、BC两边相交,画出图形求出即可;
解答: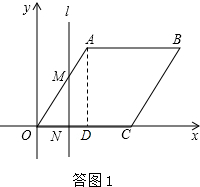 解:(1)∵OA∥CB,AB∥OC
解:(1)∵OA∥CB,AB∥OC
∴四边形OABC为平行四边形,
∵OC=OA=4,
∴平行四边形OABC为菱形,
∴OA=AB=BC=CO=4,
过A作AD⊥OC于D,如答图1
∵∠AOC=60°,
∴OD=2,AD=2
,
∴A(2,2
),B(6,2
);
(2)直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有三种情况:①如答图2,
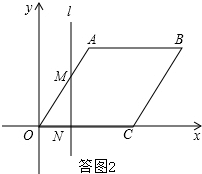
当0≤t≤2时,直线l与OA、OC两边相交,
∵MN⊥OC,
∴ON=t,
∴MN=ON•tan60°=
t,
∴S=
ON•MN=
t2;
②当2<t≤4时,直线l与AB、OC两边相交,如答图3,

S=
ON•MN=
×t×2
=
t;
③当4<t≤6时,直线l与AB、BC两边相交,如答图4,
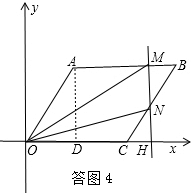
设直线l与x轴交于H,
MN=2
-
(t-4)=6
-
t,
∴S=
MN•OH=
•(6
-
t)t=-
t2+3
t;
 解:(1)∵OA∥CB,AB∥OC
解:(1)∵OA∥CB,AB∥OC∴四边形OABC为平行四边形,
∵OC=OA=4,
∴平行四边形OABC为菱形,
∴OA=AB=BC=CO=4,
过A作AD⊥OC于D,如答图1
∵∠AOC=60°,
∴OD=2,AD=2
| 3 |
∴A(2,2
| 3 |
| 3 |
(2)直线l从y轴出发,沿x轴正方向运动与菱形OABC的两边相交有三种情况:①如答图2,

当0≤t≤2时,直线l与OA、OC两边相交,
∵MN⊥OC,
∴ON=t,
∴MN=ON•tan60°=
| 3 |
∴S=
| 1 |
| 2 |
| ||
| 2 |
②当2<t≤4时,直线l与AB、OC两边相交,如答图3,

S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
③当4<t≤6时,直线l与AB、BC两边相交,如答图4,

设直线l与x轴交于H,
MN=2
| 3 |
| 3 |
| 3 |
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
点评:本题考查了菱形的性质,三角形的面积,二次函数、一次函数的应用等知识点的应用,主要考查学生综合运用性质进行计算的能力.注意一定要进行分类讨论.

练习册系列答案
相关题目
 如图为6个边长相等的正方形的组合图形,则∠1+∠3=
如图为6个边长相等的正方形的组合图形,则∠1+∠3=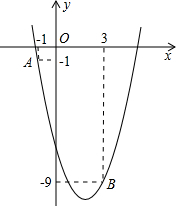 如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
如图,已知二次函数y=ax2-4x+c的图象经过点A和点B. a、b、c三个数在数轴上位置如图所示,且丨a丨=丨c丨,化简丨a丨-丨b+a丨+丨b-c丨+c+丨c+a丨=
a、b、c三个数在数轴上位置如图所示,且丨a丨=丨c丨,化简丨a丨-丨b+a丨+丨b-c丨+c+丨c+a丨=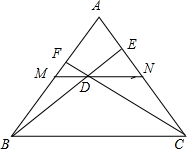 如图,在等边△ABC中,M、N分别是AB、AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F,求证:
如图,在等边△ABC中,M、N分别是AB、AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F,求证: