题目内容
7.如图1,点A,B是在数轴上对应的数字分别为-12和4,动点P和Q分别从A,B两点同时出发向右运动,点P的速度是5个单位/秒,点Q的速度是2个单位/秒,设运动时间为t秒.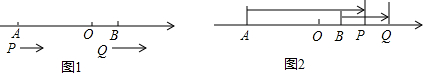
(1)AB=16.
(2)当点P在线段BQ上时(如图2):
①BP=5t-16(用含t的代数式表示);
②当P点为BQ中点时,求t的值.
分析 (1)根据数轴上两点间的距离公式结合A、B两点表示的数,即可得出结论;
(2)①根据“路程=速度×时间”“表示出来线段AP的长,再根据线段之间的关系即可得出结论;
②根据“路程=速度×时间”“表示出来线段BQ的长,再结合①的结论即可得出关于时间t的一元一次方程,解方程即可得出结论.
解答 解:(1)∵点A,B是在数轴上对应的数字分别为-12和4,
∴AB=4-(-12)=16.
故答案为:16.
(2)①∵点P从点A出发向右以5个单位/秒的速度运动,
∴AP=5t,
∵AP=AB+BP,且AB=16,
∴BP=AP-AB=5t-16.
故答案为:5t-16.
②∵点Q从点B出发向右以2个单位/秒的速度运动,
∴BQ=2t,
∵P点为BQ中点,且BP=5t-16,
∴2t=2×(5t-16),
解得:t=4.
故当P点为BQ中点时,t的值为4.
点评 本题考查了一元一次方程的应用以及数轴上两点间的距离公式,解题的关键是:(1)根据两点间的距离公式求出线段AB的长;(2)①根据数量关系表示出AP的长度;②根据数量关系表示出BQ的长度.本题属于基础题,难度不大,解决该题型题目时,结合数量关系表示出线段的长度,再根据线段间的关系列出方程是关键.

练习册系列答案
相关题目
16.下列式子正确的是( )
| A. | 5$<\sqrt{5}$ | B. | -$\sqrt{5}$$>-\sqrt{3}$ | C. | $\sqrt{5}-3$$<3-\sqrt{5}$ | D. | 0$<\sqrt{5}-3$ |

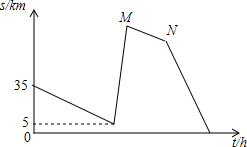 甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题:
甲、乙两车准备从A地开往B地,由于甲车比乙车慢,所以甲车先出发半小时后乙车再追赶甲车,当乙车出发3h到达一丁字路口时,改变了行进方向,行进了40km后发现选错了行进方向,于是立即调转车头按原速继续追赶甲车,当乙车又追赶了1h后,甲车到达了B地,再行进过程中两车都保持匀速.甲、乙两车间的路程s(单位:km)与乙车行驶的时间t(单位:h)之间的函数图象如图所示,请根据图象信息解答下列问题: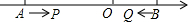 如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.