题目内容
 如图,二次函数y=ax2+bx+c的图象,此抛物线与x轴交点的横坐标为-1和3,则在下列结论错误的是( )
如图,二次函数y=ax2+bx+c的图象,此抛物线与x轴交点的横坐标为-1和3,则在下列结论错误的是( )| A、方程ax2+bx+c=0的两根和为2 |
| B、b>0 |
| C、a+b+c<0 |
| D、4a2-2b+c>0 |
考点:抛物线与x轴的交点,二次函数图象与系数的关系
专题:
分析:与x轴的交点坐标为(-1,0),(3,0),则方程ax2+bx+c=0的根为x1=-1,x2=3,两根和为2;抛物线开口向上则a>0,对称轴在y轴右侧,则b<0;当x=1时,y=a+b+c<0;当x=-2时,y=4a-2b+c>0.
解答:解:∵抛物线与x轴的交点坐标为(-1,0),(3,0),
∴方程ax2+bx+c=0的根为x1=-1,x2=3,故A正确;
由图象得,a>0,c<0,b<0,故B错误;
∵对称轴为x=1,
∴a+b+c<0,故C正确;
∵x=-2时,y>0,即4a-2b+c>0,
故D正确.
故选:B.
∴方程ax2+bx+c=0的根为x1=-1,x2=3,故A正确;
由图象得,a>0,c<0,b<0,故B错误;
∵对称轴为x=1,
∴a+b+c<0,故C正确;
∵x=-2时,y>0,即4a-2b+c>0,
故D正确.
故选:B.
点评:此题考查了抛物线和x轴的交点坐标问题,解题的关键是判断a,b,c的符号,此题较复杂,要熟练掌握.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若2a2-3a-5=0,则4a4-12a3+9a2-10的值为( )
| A、10 | B、0 | C、15 | D、5 |
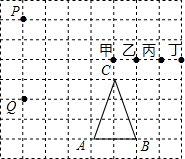 如图所示,若ABCPQ甲乙丙丁都是方格纸中的格点.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( )
如图所示,若ABCPQ甲乙丙丁都是方格纸中的格点.如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的( )| A、甲 | B、乙 | C、丙 | D、丁 |
与
是同类二次根式的是( )
| 3 |
A、2
| ||
B、
| ||
| C、3 | ||
D、
|
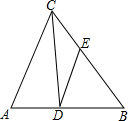 如图,在△ABC中,∠ACB的平分线交AB于点D,DE∥AC交BC于点E,若AC=9,CE=3,求BE的长.
如图,在△ABC中,∠ACB的平分线交AB于点D,DE∥AC交BC于点E,若AC=9,CE=3,求BE的长. 已知,如图,Rt△ACB中,∠ACB=90°,AC=kBC,P为AB上一点,作∠EPF=90°,分别交AC、CB的延长线于E、F两点.若PA=mPB,试判断PE、PF的数量关系,并说明理由.
已知,如图,Rt△ACB中,∠ACB=90°,AC=kBC,P为AB上一点,作∠EPF=90°,分别交AC、CB的延长线于E、F两点.若PA=mPB,试判断PE、PF的数量关系,并说明理由.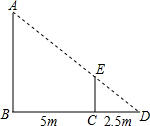 如图,身高为1.6m的小亮想测量一棵大树(AB)的高度,他沿着树影(BD)由点B向点D走动,当走到点C时,他的影子顶端正好与树的影子顶端重合(于点D),测得BC=5m,CD=2.5m,则树的高度为
如图,身高为1.6m的小亮想测量一棵大树(AB)的高度,他沿着树影(BD)由点B向点D走动,当走到点C时,他的影子顶端正好与树的影子顶端重合(于点D),测得BC=5m,CD=2.5m,则树的高度为


