题目内容
18. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.(1)猜想:△ABD与△ADC的面积有何关系?并简要说明理由;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
分析 (1)作AF⊥BC,根据三角形的面积得出等底等高的三角形面积相等分析即可;
(2)根据高的做法作出图形即可;
(3)根据三角形的面积解答即可.
解答 解:(1)△ABD与△ADC的面积相等,理由如下:
作AF⊥BC,如图1: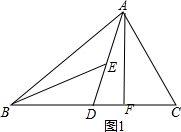
因为BD=DC,AF=AF,
所以△ABD与△ADC的面积相等;
(2)作图,如图2: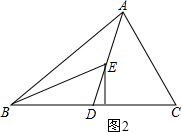
(3)因为△ABC的面积为40,BD=5,
所以△ABD的面积为20,
因为BE为△ABD的中线,
所以△BDE的面积为10,
所以△BDE中BD边上的高为4.
点评 此题考查三角形的面积,关键是根据三角形的中线把三角形分成两个面积相等的两部分分析.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
8.下列算式正确的是( )
| A. | -2+1=-3 | B. | (-$\frac{1}{4}$)÷(-4)=1 | C. | -32=9 | D. | -5-(-2)=-3 |
7.直角三角形一条直角边和斜边的长分别是一元二次方程x2-9x+20=0的两个实数根,则该三角形的面积是( )
| A. | 6 | B. | 6或10 | C. | 10 | D. | 12 |
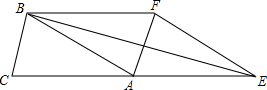 如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA的长度得到△EFA.连结BF,BE.
如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA的长度得到△EFA.连结BF,BE. 如图,在△ABC中,∠C=40°,CA=CB,过A点作EA∥BC,则∠EAB=70°.
如图,在△ABC中,∠C=40°,CA=CB,过A点作EA∥BC,则∠EAB=70°.