题目内容
解方程:
-
=
-
.
| x+1 |
| x+2 |
| x+2 |
| x+3 |
| x+5 |
| x+6 |
| x+6 |
| x+7 |
考点:解分式方程
专题:计算题
分析:分式方程变形,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:方程变形得:
-
=
-
,
即1-
-1+
=1-
-1+
,
整理得:
-
=
-
,即
=
,
整理得:
=
,
去分母得:x2+5x+6=x2+13x+42,
解得:x=-4.5,
经检验是分式方程的解.
| x+2-1 |
| x+2 |
| x+3-1 |
| x+3 |
| x+6-1 |
| x+6 |
| x+7-1 |
| x+7 |
即1-
| 1 |
| x+2 |
| 1 |
| x+3 |
| 1 |
| x+6 |
| 1 |
| x+7 |
整理得:
| 1 |
| x+3 |
| 1 |
| x+2 |
| 1 |
| x+7 |
| 1 |
| x+6 |
| x+2-x-3 |
| (x+2)(x+3) |
| x+6-x-7 |
| (x+6)(x+7) |
整理得:
| 1 |
| x2+5x+6 |
| 1 |
| x2+13x+42 |
去分母得:x2+5x+6=x2+13x+42,
解得:x=-4.5,
经检验是分式方程的解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
在平面直角坐标系中,点(4,-3)关于y轴对称的点的坐标是( )
| A、(-4,-3) |
| B、(4,3) |
| C、(-4,3) |
| D、(4,-3) |
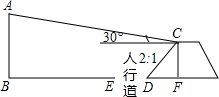 城市规划期间,欲拆除一电线杆AB(如图),已知距电线杆AB水平距离14m的D处有一大坝,背水坝CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道.求BF长.
城市规划期间,欲拆除一电线杆AB(如图),已知距电线杆AB水平距离14m的D处有一大坝,背水坝CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道.求BF长.