题目内容

4．一个不透明袋中放入7枚只有颜色不同的围棋棋子，其中4枚黑色，3枚白色，任意摸出一枚，摸到棋子是黑色的概率为$\frac{4}{7}$．

分析 根据概率公式用黑色棋子的个数除以总棋子的个数即可．

解答 解：∵共有7枚棋子，其中4枚黑色，3枚白色，
∴摸到棋子是黑色的概率为$\frac{4}{7}$；
故答案为：$\frac{4}{7}$．

点评 本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．

练习册系列答案
相关题目
17．如图，点B、F、C、E在一条直线上，∠B=∠E，AC∥FD，BF=CE．求证：AB=DE．
15．阅读材料：
我们曾经解决过如下问题：“如图1，点M，N分别在直线AB同侧，如何在直线AB上找到一个点P，使得PM+PN最小？”
我们可以经过如下步骤解决这个问题：
（1）画草图（或目标图）分析思路：在直线AB上任取一点P′，连接P′M，P′N，根据题目需要，作点M关于直线AB的对称点M′，将P′M+P′N转化为P′M′+P′N′，“化曲为直”寻找P′M′+P′N的最小值；
（2）设计画图步骤；
（3）回答结论并验证．
解决下列两个问题：
（1）如图2，在△ABC中，AB=3，AC=4，BC=5，EF垂直且平分BC，点P在直线EF上，直接写出PA+PB的最小值，回答PA+PB取最小值时点P的位置并在图中标出来；解：PA+PB的最小值为4，PA+PB取最小值时点P的位置是线段CA与直线EF的交点；
（2）如图3，点M，N分别在直线AB两侧，在直线AB上找一点P，使得∠MPB=∠NPB．要求画图，并简要叙述确定点P位置的步骤．（无需尺规作图，保留画图痕迹，无需证明）
解：确定点P位置的简要步骤：先画点M关于直线AB的对称点M'，射线NM'与直线AB的交点即为点P．
12．下列说法正确的是（　　）
A．2πx2的系数是2B．-xy2的次数为2C．-5x2+x=-4x3D．3x2-x2=2x2
19．一种圆环（如图所示），它的外圆直径是8厘米，环宽1厘米

①如果把这样的2个圆环扣在一起并拉紧（如图2），长度为14厘米
②如果用x个这样的圆环相扣并拉紧，长度为y厘米，则y与x之间的关系式是y=6x+2．
9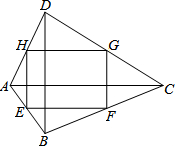．如图，四边形ABCD中，AC=8，BD=6，且AC⊥BD，连接四边形ABCD各边中点得到四边形EFGH，下列说法正确的是（　　）
A．四边形EFGH是矩形B．四边形EFGH的周长是7
C．四边形EFGH的面积是24D．四边形ABCD的面积是48
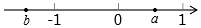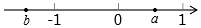16．有理数a，b在数轴上对应的位置如图所示，则下列结论成立的是（　　）
A．a+b＞0B．a-b＞0C．ab＞0D．$\frac{a}{b}＞0$
13．如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（　　）
A．∠A=∠DB．AC=BDC．∠ACB=∠DBCD．AB=DC
11．当x＜1时，分式$\frac{-1}{x-1}$的值为正数．当x=-2时，$\frac{{x}^{2}-4}{x-2}$的值为零．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网