题目内容
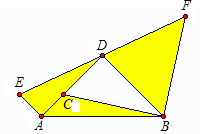 如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD=
如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD=| 2 |
考点:旋转的性质,等腰直角三角形
专题:
分析:作CM⊥AB,DN⊥BF垂足分别为M,N,由△ABD为等腰直角三角形,已知AD=BD=
,由勾股定理,得AB=2,设AC=x,则AE=AM=CM=
x,由此可分别表示S△AED和S△ABC,利用S△BFD=
BF×DN,根据∠NDB+∠DBN=90°,∠DBN+∠CBD=90°,可证∠NDB=∠CBD,可证△BDN∽△CBD,利用相似比将BF×DN=DN×BC进行转化,继而可求得S△AED+S△BFD-S△ABC的值.
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答: 解:作CM⊥AB,DN⊥BF垂足分别为M,N,
解:作CM⊥AB,DN⊥BF垂足分别为M,N,
由旋转的性质可知AC=AE,BC=BF,
设AC=x,
∵△ABD是等腰直角三角形,
∴∠DAB=45°,
∴AE=AM=CM=AC•sin45°=
x,
又∵AD=BD=
,
∴AB=
=2,
∴S△AED=
×AE×AD=
x,S△ABC=
×AB×CM=
x,
∵∠DBC+∠DCB=90°,∠DBC+∠DBN=90°,
∴∠DCB=∠DBBN,
∵∠DNB=∠BDC=90°,
∴△BDN∽△CBD,
∴DN:BD=BD:BC,
∴DN×BC=BD2=2,
∴S△BFD=
×BF×DN=
×DN×BC=1,
∴S△AED+S△BFD-S△ABC=
x+1-
x=1.
故答案为:1.
 解:作CM⊥AB,DN⊥BF垂足分别为M,N,
解:作CM⊥AB,DN⊥BF垂足分别为M,N,由旋转的性质可知AC=AE,BC=BF,
设AC=x,
∵△ABD是等腰直角三角形,
∴∠DAB=45°,
∴AE=AM=CM=AC•sin45°=
| ||
| 2 |
又∵AD=BD=
| 2 |
∴AB=
| AD2+BD2 |
∴S△AED=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵∠DBC+∠DCB=90°,∠DBC+∠DBN=90°,
∴∠DCB=∠DBBN,
∵∠DNB=∠BDC=90°,
∴△BDN∽△CBD,
∴DN:BD=BD:BC,
∴DN×BC=BD2=2,
∴S△BFD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AED+S△BFD-S△ABC=
| ||
| 2 |
| ||
| 2 |
故答案为:1.
点评:本题考查了旋转的性质,三角形面积的表示方法,相似三角形的判定与性质的运用.注意旋转前后对应角相等,对应边相等,旋转角为对应点与旋转中心连线的夹角.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
若不论k取什么实数,关于x的方程
-
=1(a、b是常数)的根总是x=1,则a+b=( )
| 2kx+a |
| 3 |
| x-bk |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
有一个六边形的半径为4cm,则这个六边形的面积为( )
A、6
| ||
B、12
| ||
C、24
| ||
D、48
|
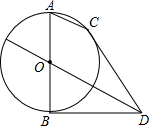 已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD,
已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD,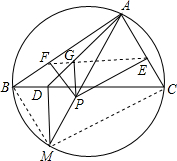 如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.
如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线. 已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为
已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为