题目内容
 已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为1,2,
已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为1,2,| 2 |
考点:旋转的性质,勾股定理,勾股定理的逆定理,正方形的性质
专题:计算题
分析:将△APD绕点A顺时针旋转90°得到△AP′B,过A作AN⊥BP′于N,得出等腰直角三角形APP′,求出PP′,求出直角三角形BPP′,求出等腰直角三角形ANP′,求出AN,根据勾股定理求出AB的值,即可求出正方形的面积.
解答: 解:将△APD绕点A顺时针旋转90°得到△AP′B,则P′A=1,P′B=
解:将△APD绕点A顺时针旋转90°得到△AP′B,则P′A=1,P′B=
,
则△APP′是等腰直角三角形,PP′=
,∠AP′P=45°,
∵PP′2+P′B2=(
)2+(
) 2=4,PB2=4,
∴PP′2+P′B2=PB2,
∴△PP′B是等腰直角三角形,
∴∠PP′B=90°,
过A作AN⊥BP′于N,
则∠AP′N=180°-90°-45°=45°,
即△ANP′是等腰直角三角形,
由勾股定理得:AN=NP′=
,
由勾股定理得:AB2=AN2+BN2,
=(
)2+(
+
) 2,
=5,
∴正方形ABCD的面积是5.
 解:将△APD绕点A顺时针旋转90°得到△AP′B,则P′A=1,P′B=
解:将△APD绕点A顺时针旋转90°得到△AP′B,则P′A=1,P′B=| 2 |
则△APP′是等腰直角三角形,PP′=
| 2 |
∵PP′2+P′B2=(
| 2 |
| 2 |
∴PP′2+P′B2=PB2,
∴△PP′B是等腰直角三角形,
∴∠PP′B=90°,
过A作AN⊥BP′于N,
则∠AP′N=180°-90°-45°=45°,
即△ANP′是等腰直角三角形,
由勾股定理得:AN=NP′=
| ||
| 2 |
由勾股定理得:AB2=AN2+BN2,
=(
| ||
| 2 |
| ||
| 2 |
| 2 |
=5,
∴正方形ABCD的面积是5.
点评:本题考查了正方形性质,勾股定理,勾股定理的逆定理,等腰直角三角形,旋转的性质等知识点的应用,解此题的关键是正确作辅助线,本题具有一定的代表性,有一定的难度,对学生提出较高的要求.

练习册系列答案
相关题目
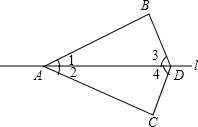 如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )
如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )| A、AB=AC |
| B、∠3=∠4 |
| C、∠B=∠C |
| D、BD=CD |
 如图,已知△ABC中,∠B=90°,AB=3,BC=
如图,已知△ABC中,∠B=90°,AB=3,BC=| 3 |
| 6 |
| A、10° | B、15° |
| C、20° | D、25° |
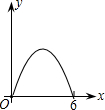
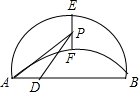 如图弧AEB与弧AFB有公共弦AB=6,D是弦AB上的一点,AD=x,点E、F分别是弧AEB与弧AFB的中点,P是EF上的中点,y=AP2-DP2,则y与x的函数关系式是( )
如图弧AEB与弧AFB有公共弦AB=6,D是弦AB上的一点,AD=x,点E、F分别是弧AEB与弧AFB的中点,P是EF上的中点,y=AP2-DP2,则y与x的函数关系式是( )

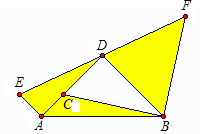 如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD=
如图,等腰直角三角形ABD,点C是直角边AD上的动点,连接CB.现在将点C绕点A逆时针方向旋转90°得点E,再将点C绕点B顺时针方向旋转90°得点F.如果AD=BD= 如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为
如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为 如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为
如图,两个同心圆,大圆的弦AB切小圆于点C,且AB=10,则图中阴影部分面积为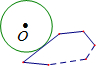 如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈.
如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈.