题目内容
四边形ABCD是平行四边形，点E，F在直线BD上，且DE=BF，试猜想∠AEC和∠AFC的关系，并说明理由．考点：平行四边形的性质
专题：
分析：首先连接AC，交BD于O，根据平行四边形的性质可得DO=BO，AO=CO，再由DE=BF，可得EO=FO，再根据对角线互相平分的四边形是平行四边形可得四边形AECF是平行四边形，再根据平行四边形对角相等可得∠AEC=∠AFC．
解答：
解：∠AEC=∠AFC，
连接AC，交BD于O，
∵四边形ABCD是平行四边形，
∴DO=BO，AO=CO，
∵DE=BF，
∴EO=FO，
∴四边形AECF是平行四边形，
∴∠AEC=∠AFC．
解：∠AEC=∠AFC，连接AC，交BD于O，
∵四边形ABCD是平行四边形，
∴DO=BO，AO=CO，
∵DE=BF，
∴EO=FO，
∴四边形AECF是平行四边形，
∴∠AEC=∠AFC．
点评：此题主要考查了平行四边形的性质，关键是掌握平行四边形的对角线互相平分，平行四边形的对角相等．
练习册系列答案
相关题目
如图，如果半径为1个单位长度的圆上有一点A，且点A与数轴上表示5.1的点重合（圆与数轴只有这一个交点），让圆沿数轴的负方向滚动一周，点A到达另一点B，则A，B两点之间表示整数的点共有（ ）
如图，直线y=ax+b（a≠0）与y=cx+d（c≠0）相交于点P，则关于x，y的方程组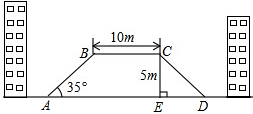
如图，为了缓解交通拥堵，方便行人，在某街道计划修建一座横断面为梯形ABCD的过街天桥．天桥斜坡AB的坡角∠BAD为35°，斜坡CD的坡度为i=1：1.2（垂直高度CE与水平宽度DE的比），上底BC=10m，天桥高度CE=5m，求天桥下底AD的长度？（结果精确到0.1m，参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
如图，某公路上A，B两点的正南方有D，C两村庄，现要在公路AB上建一个车站E，使C，D两村到E站的距离相等，已知AB=50km，DA=20km，CB=10km，请你设计出E站的位置，并计算车站E距A点多远？
如图，已知CD⊥AB于点D，FE⊥AB于点E，且∠1=∠2，∠3=84°，求∠ACB的度数．