题目内容
7．某工艺品厂生产一款工艺品，已知这款工艺品的生产成本为每件60元，经市场调研发现：该款工艺品每天的销量y件与售价x之间存在着如下表所示的一次函数关系．| 售价x元 | … | 70 | 90 | … |
| 销售量y件 | … | 3000 | 1000 | … |
（2）设每天获得的利润为w元，当售价x为多少时，每天获得利润最大？并求出最大值．
分析 （1）设y与x的函数关系为y=kx+b，再把x=70，y=3000，x=90，y=1000代入可得关于k、b的方程组，解可得k、b的值，进而可得函数解析式；
（2）根据总利润=销量×售价可得w=（x-60）（-100x+10000），然后求出函数的最值即可．
解答 解：（1）设y与x的函数关系为y=kx+b，
$\left\{\begin{array}{l}{70k+b=3000}\\{90k+b=1000}\end{array}\right.$，
∴k=-100，b=10000，
∴y=-100x+10000；
（2）依题意得：w=（x-60）（-100x+10000）=-100x2+16000x-600000，
∵函数开口向下，
∴有最大值，
∴当x=-$\frac{b}{2a}$=80时，w最大=40000；
所以当售价x为80元时，每天获得的利润最大，最大值为40000元．
点评 此题主要考查了二次函数的应用，关键是正确理解题意，找出题目中的等量关系，利用待定系数法求出销售量y件与售价x元之间的函数关系式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某研究性学习小组，为了测量某池塘边A、B两点间的距离，让一架航模在直线AB的正上方24米的高度飞行，当航模位于点D处时，在A点处测得航模仰角为60°，5分钟后，当航模在点C处时，在B点测得航模仰角为45°，己知航模飞行的速度为每分钟45米，试计算A、B两点的距离．（结果精确到0.1米，参考数据：$\sqrt{2}=1.41，\sqrt{3}$=1.73．）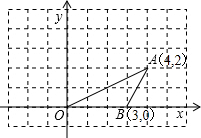
如图，点O、A、B的坐标分别为（0，0）、（4，2）、（3，0），将△OAB绕点O按逆时针方向旋转90°后，得到△OCD．（点A转到点C）
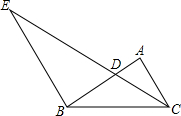如图，点D为△ABC的边AB上的一点，连结CD，过点B作BE∥AC交CD的延长线于点E，且∠ACD=∠DBC，S△ADC：S△BED=4：9，AB=10，则AC的长为2$\sqrt{10}$．
（1）根据图中的规律，写出a7；
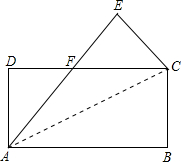已知：将长方形ABCD沿直线AC对折，将点B折到点E处，AE交CD于点F，
甲、乙两人沿相同的路线由A地到B地匀速前进，A，B两地间的路程为20千米，他们前进的路程为s（单位：千米），甲出发后的时间为t（单位：小时），甲、乙前进的路程与时间的函数图象如图所示．根据图象信息回答下列问题：