题目内容
15.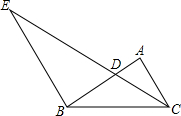 如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长为2$\sqrt{10}$.
如图,点D为△ABC的边AB上的一点,连结CD,过点B作BE∥AC交CD的延长线于点E,且∠ACD=∠DBC,S△ADC:S△BED=4:9,AB=10,则AC的长为2$\sqrt{10}$.
分析 证明△ADC∽△BED,根据相似三角形的面积的比等于相似比的平方求得BD和AD的长,然后证明△ADC∽△ACB,根据相似三角形的对应边的比相等求解.
解答 解:∵BE∥AC,
∴△ADC∽△BED,
∴$\frac{BD}{AD}$=$\sqrt{S△ADC:S△BED}$=$\frac{2}{3}$.
又∵AB=10,
∴BD=6,AD=4.
∵∠ACD=∠DBC,∠A=∠A,
∴△ADC∽△ACB,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,
∴AC2=AB•AD=10×4=40,
∴AC=2$\sqrt{10}$.
故答案是:2$\sqrt{10}$.
点评 本题考查了相似三角形的判定与性质,相似三角形的对应边的比相等,面积的比等于相似比的平方,求得BD和AD的长是关键.

练习册系列答案
相关题目
3.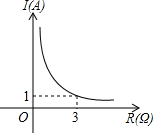 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )| A. | $I=\frac{2}{R}$ | B. | $I=\frac{3}{R}$ | C. | $I=\frac{5}{R}$ | D. | $I=\frac{6}{R}$ |
7.某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为每件60元,经市场调研发现:该款工艺品每天的销量y件与售价x之间存在着如下表所示的一次函数关系.
(1)求销售量y件与售价x元之间的函数关系式;
(2)设每天获得的利润为w元,当售价x为多少时,每天获得利润最大?并求出最大值.
| 售价x元 | … | 70 | 90 | … |
| 销售量y件 | … | 3000 | 1000 | … |
(2)设每天获得的利润为w元,当售价x为多少时,每天获得利润最大?并求出最大值.
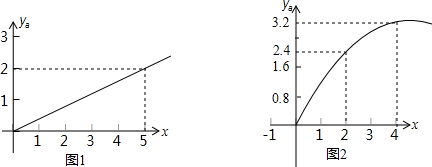
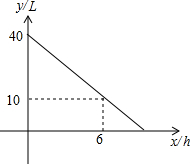 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.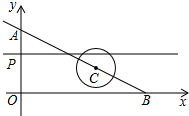 如图,直线AB的解析式为y=-$\frac{{\sqrt{3}}}{3}$x+6分别与x轴、y轴相交于B、A两点.点C在射线BA上以3cm/秒的速度运动,以C点为圆心作半径为1cm的⊙C.点P以2cm/秒的速度在线段OA上来回运动,过点P作直线l垂直于y轴.若点C与点P 同时从点B、点O开始运动,设运动时间为t秒,试求:
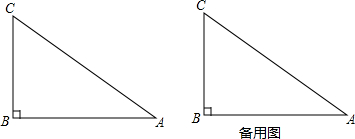
如图,直线AB的解析式为y=-$\frac{{\sqrt{3}}}{3}$x+6分别与x轴、y轴相交于B、A两点.点C在射线BA上以3cm/秒的速度运动,以C点为圆心作半径为1cm的⊙C.点P以2cm/秒的速度在线段OA上来回运动,过点P作直线l垂直于y轴.若点C与点P 同时从点B、点O开始运动,设运动时间为t秒,试求: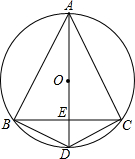 如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.
如图,△ABC是⊙O的内接等腰三角形,其顶角的平分线AD交⊙O于D,交BC于E,连接BD,DC.