题目内容
19.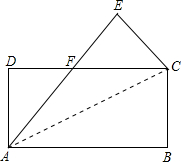 已知:将长方形ABCD沿直线AC对折,将点B折到点E处,AE交CD于点F,
已知:将长方形ABCD沿直线AC对折,将点B折到点E处,AE交CD于点F,(1)求证:△ACF是等腰三角形;
(2)若CD=16cm,AD=8cm,求△ACF的面积.
分析 (1)由折叠得到一对角相等,再利用两直线平行得到一对内错角相等,等量代换及等角对等边得到AF=CF,得证;
(2)设DF=xcm,可得出AF=FC=(16-x)cm,在直角三角形ADF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出FC的长,即可求出三角形ACF面积.
解答 (1)证明:∵将长方形ABCD沿直线AC对折,将点B折到点E处,
∴∠EAC=∠BAC,
∵长方形ABCD,即DC∥AB,
∴∠DCA=∠BAC,
∴∠EAC=∠DCA,
∴AF=CF,
则△ACF为等腰三角形;
(2)解:设DF=xcm,则AF=CF=CD-DF=(16-x)cm,
在Rt△ADF中,根据勾股定理得:AF2=AD2+DF2,
即(16-x)2=82+x2,
解得:x=6,
∴CF=16-6=10cm,
则S△ACF=$\frac{1}{2}$CF•AD=40cm2.
点评 此题考查了折叠变换,平行线的性质,等腰三角形的判定,勾股定理,以及三角形面积求法,熟练掌握折叠的性质是解本题的关键.

练习册系列答案
相关题目
7.某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为每件60元,经市场调研发现:该款工艺品每天的销量y件与售价x之间存在着如下表所示的一次函数关系.
(1)求销售量y件与售价x元之间的函数关系式;
(2)设每天获得的利润为w元,当售价x为多少时,每天获得利润最大?并求出最大值.
| 售价x元 | … | 70 | 90 | … |
| 销售量y件 | … | 3000 | 1000 | … |
(2)设每天获得的利润为w元,当售价x为多少时,每天获得利润最大?并求出最大值.
9.2014年12月10日从省教厅获悉,今年起我省编制并实施全面改善贫困地区义务教育薄弱学校基本办学条件计划《实施方案》,目前,已安排下达2014年“全面改薄”中央专项资金19.4亿元.用科学记数法表示19.4亿为( )
| A. | 19.4×108 | B. | 1.94×108 | C. | 1.94×109 | D. | 19.4×109 |
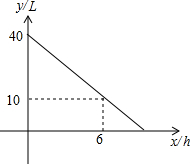 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.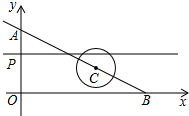 如图,直线AB的解析式为y=-$\frac{{\sqrt{3}}}{3}$x+6分别与x轴、y轴相交于B、A两点.点C在射线BA上以3cm/秒的速度运动,以C点为圆心作半径为1cm的⊙C.点P以2cm/秒的速度在线段OA上来回运动,过点P作直线l垂直于y轴.若点C与点P 同时从点B、点O开始运动,设运动时间为t秒,试求:
如图,直线AB的解析式为y=-$\frac{{\sqrt{3}}}{3}$x+6分别与x轴、y轴相交于B、A两点.点C在射线BA上以3cm/秒的速度运动,以C点为圆心作半径为1cm的⊙C.点P以2cm/秒的速度在线段OA上来回运动,过点P作直线l垂直于y轴.若点C与点P 同时从点B、点O开始运动,设运动时间为t秒,试求: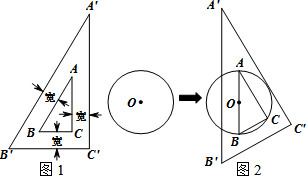
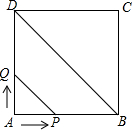 如图,正形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,当P、Q到达点C时都停止运动.设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2).
如图,正形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,当P、Q到达点C时都停止运动.设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2).