题目内容
2.某商场销售一批品牌衬衫,平均每天售出20件,每件可盈利40元.为了扩大销售增加盈利,尽快减少库存,商场决定采取适当降价措施.调查发现,每件少盈利1元,商场平均每天可多售出2件衬衫.那么每件衬衫少盈利多少元时,商场平均每天盈利最多?分析 首先根据题意,设每件衬衫少盈利x元,商场平均每天盈利y元,则每件盈利40-x元,每天可以售出20+2x件,所以商场平均每天盈利(40-x)(20+2x)元,即y=(40-x)(20+2x);然后用“配方法”求出y的最大值,并求出每件衬衫少盈利多少元即可.
解答 解:设每件衬衫少盈利x元,商场平均每天盈利y元,
则y=(40-x)(20+2x)
=800+80x-20x-2x2
=-2x2+60x+800
=-2(x2-30x+225)+800+450
=-2(x-15)2+1250
所以当x=15时,y的最大值为1250,
即每件衬衫少盈利15元时,商场平均每天盈利最多,是1250元.
答:每件衬衫少盈利15元时,商场平均每天盈利最多,是1250元.
点评 (1)此题主要考查了一元二次方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键.
(2)此题还考查了“配方法”在求函数的最大值的问题中的应用,要熟练掌握.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为( )
| A. | y=x | B. | y=x-1 | C. | y=x+1 | D. | y=-x+1 |
7.某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为每件60元,经市场调研发现:该款工艺品每天的销量y件与售价x之间存在着如下表所示的一次函数关系.
(1)求销售量y件与售价x元之间的函数关系式;
(2)设每天获得的利润为w元,当售价x为多少时,每天获得利润最大?并求出最大值.
| 售价x元 | … | 70 | 90 | … |
| 销售量y件 | … | 3000 | 1000 | … |
(2)设每天获得的利润为w元,当售价x为多少时,每天获得利润最大?并求出最大值.
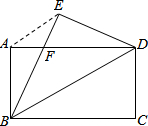 如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.
如图,在矩形纸片ABCD中,AB=6,BC=8将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连结AE.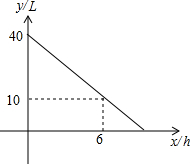 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.
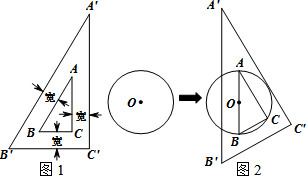
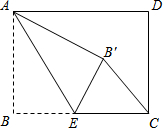 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.